Giải chi tiết Câu hỏi Hoạt động 1 trang 5 SGK Toán 12 Cánh diều – Bài 1. Tính đơn điệu của hàm số. Tham khảo: Dựa vào định nghĩa hàm số đồng biến.
Câu hỏi/Đề bài:
a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập \(K \subset \mathbb{R}\), trong đó K là một khoảng, đoạn hoặc nửa khoảng.
b) Cho hàm số \(y = f\left( x \right) = {x^2}\) có đồ thị như Hình 2.
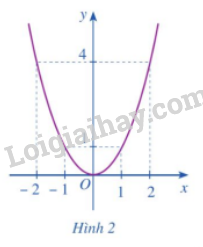
– Xác định khoảng đồng biến, nghịch biến của hàm số đó.
– Xét dấu đạo hàm \(f’\left( x \right) = 2x\).
– Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^2}\) và dấu của đạo hàm \(f’\left( x \right) = 2x\) trên mỗi khoảng \(\left( { – \infty ;0} \right),\left( {0; + \infty } \right)\).
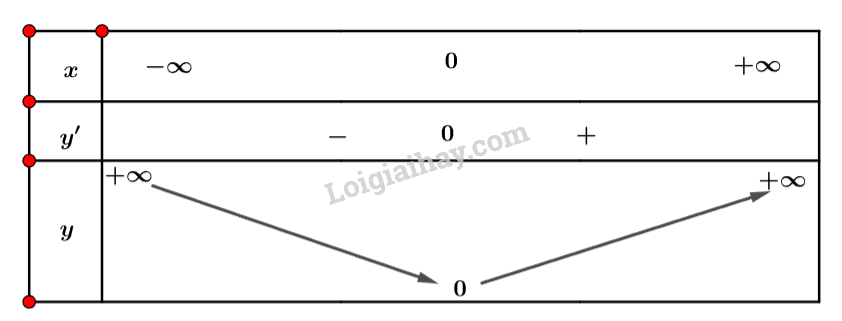
– Hoàn thành bảng biến thiên sau:
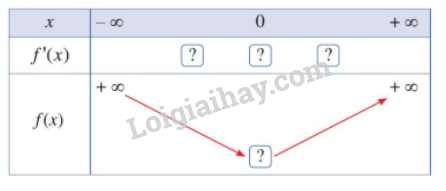
Hướng dẫn:
Dựa vào định nghĩa hàm số đồng biến, nghịch biến trên tập K
Lời giải:
a) Cho K là một khoảng, một đoạn hoặc một nửa khoảng và \(f\left( x \right)\) là hàm số xác định trên K.
– Hàm số \(f\left( x \right)\) được gọi là hàm số đồng biến trên K nếu với mọi \({x_1},{x_2}\) thuộc K và \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
– Hàm số \(f\left( x \right)\) được gọi là hàm số đồng biến trên K nếu với mọi \({x_1},{x_2}\) thuộc K và \({x_1} f\left( {{x_2}} \right)\).
– Hàm số đồng biến hoặc nghịch biến trên K còn được gọi là hàm số đơn điệu trên K.
b)
– Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { – \infty ;0} \right)\).
– Đạo hàm \(f’\left( x \right) = 2x\)âm khi \(x 0\).
– Hàm số \(y = f\left( x \right) = {x^2}\) nghịch biến khi \(f’\left( x \right) = 2x\)mang dấu âm và đồng biến khi \(f’\left( x \right) = 2x\) mang dấu dương.
– Ta có bàng biến thiên sau: