Thay các giá trị vào hàm số và giải hệ phương trình b) Tính quãng đường thông qua tích phân của vận tốc. Giải và trình bày phương pháp giải Giải bài tập 10 trang 43 SGK Toán 12 tập 2 – Cánh diều – Bài tập cuối chương 4. Một chiếc xe ô tô chạy thử nghiệm trên một đường thẳng bắt đầu từ trạng thái đứng yên….
Đề bài/câu hỏi:
Một chiếc xe ô tô chạy thử nghiệm trên một đường thẳng bắt đầu từ trạng thái đứng yên. Tốc độ của chiếc xe ô tô đó (tính bằng mét/giây) lần lượt ở giây thứ 10, thứ 20, thứ 30, thứ 40, thứ 50 và thứ 60 được ghi lại trong Bảng 1
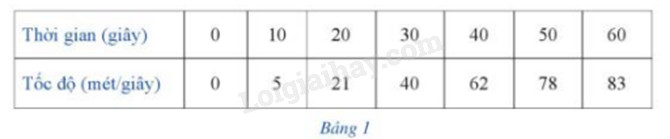
a) Hãy xây dựng hàm số bậc ba \(y = f(x) = a{x^3} + b{x^2} + cx + d(a \ne 0)\) để biểu diễn các số liệu ở Bảng 1, tức là ở hệ trục tọa độ Oxy, đồ thị của hàm số đó trên nửa khoảng \([0; + \infty )\) “gần” với các điểm O(0;0), B(10;5), C(20;21), D(30;40), E(40;62), G(50;78), K(60;83)
b) Hãy tính (gần đúng) quãng đường mà xe ô tô đó đã đi được tính đến giây thứ 60 của quá trình thử nghiệm
Hướng dẫn:
a) Thay các giá trị vào hàm số và giải hệ phương trình
b) Tính quãng đường thông qua tích phân của vận tốc
Lời giải:
a) \(v(t) = a{t^3} + b{t^2} + ct + d(a \ne 0)\) với t là thời gian (giây)
Ta có:
\(\left\{ \begin{array}{l}v(0) = d = 0\\v(10) = 1000a + 100b + 10c + d = 5\\v(20) = 8000a + 400b + 20c + d = 21\\v(30) = 27000a + 900b + 30c + d = 40\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}d = 0\\a = – \frac{1}{{750}}\\b = \frac{{19}}{{200}}\\c = – \frac{{19}}{{60}}\end{array} \right.\)
Vậy \(v(t) = – \frac{1}{{750}}{t^3} + \frac{{19}}{{200}}{t^2} – \frac{{19}}{{60}}t\)
b) Quãng đường mà xe ô tô đó đã đi được tính đến giây thứ 60 của quá trình thử nghiệm là:
\(\int\limits_0^{60} {v(t)} dt = \int\limits_0^{60} {\left( { – \frac{1}{{750}}{t^3} + \frac{{19}}{{200}}{t^2} – \frac{{19}}{{60}}t} \right)dt} = \left. {\left( { – \frac{1}{{3000}}{t^4} + \frac{{19}}{{600}}{t^3} – \frac{{19}}{{120}}{t^2}} \right)_0^{60}} \right| = 1950m\)