Từ từng ý trong đề bài suy ra được hướng, phương, độ lớn của \(\overrightarrow x , {\rm{ }}\overrightarrow y , {\rm{ }}\overrightarrow z \. Trả lời Giải bài 2.8 trang 45 sách bài tập toán 12 – Kết nối tri thức – Bài 6. Vecto trong không gian. Một chiếc bàn cân đối được đặt trên mặt sàn nằm ngang,…
Đề bài/câu hỏi:
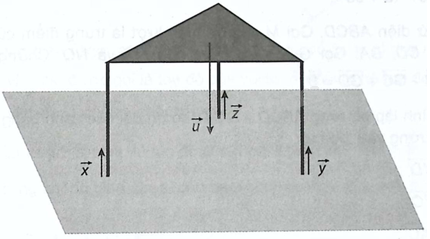
Một chiếc bàn cân đối được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn và ba chân bàn vuông góc với mặt sàn. Trọng lực tác dụng lên bàn (biểu thị bởi vectơ \(\overrightarrow u \)) phân tán đều qua các chân bàn và tạo nên các phản lực từ mặt sàn lên các chân bàn (biểu thị bởi các vectơ \(\overrightarrow x ,{\rm{ }}\overrightarrow y ,{\rm{ }}\overrightarrow z \)). Hãy giải thích vì sao \(\overrightarrow x = \overrightarrow y = \overrightarrow z = – \frac{1}{3}\overrightarrow u \).
Hướng dẫn:
Từ từng ý trong đề bài suy ra được hướng, phương, độ lớn của \(\overrightarrow x ,{\rm{ }}\overrightarrow y ,{\rm{ }}\overrightarrow z \) và mối liên hệ của chúng với trọng lực.
Lời giải:
Các vectơ \(\overrightarrow x ,{\rm{ }}\overrightarrow y ,{\rm{ }}\overrightarrow z \) đôi một cùng phương vì đều có giá vuông góc với mặt đất, cùng hướng vì chúng ngược hướng với trọng lực và chúng có độ lớn bằng nhau vì trọng lực phân tán đều qua ba chân bàn.
Do đó \(\overrightarrow x = \overrightarrow y = \overrightarrow z \) và \(\left| {\overrightarrow x } \right| = \left| {\overrightarrow y } \right| = \left| {\overrightarrow z } \right| = \frac{1}{3}\left| {\overrightarrow u } \right|\).
Vậy \(\overrightarrow x = \overrightarrow y = \overrightarrow z = – \frac{1}{3}\overrightarrow u \).