Tìm công thức \(R’\left( x \right)\). + Tìm \(x\) để \(R’\left( x \right)\) đạt giá trị lớn nhất. Trả lời Giải bài 1.42 trang 31 sách bài tập toán 12 – Kết nối tri thức – Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn. Doanh số bán hệ thống âm thanh nổi mới trong khoảng thời gian dự kiến sẽ tuân theo đường cong…
Đề bài/câu hỏi:
Doanh số bán hệ thống âm thanh nổi mới trong khoảng thời gian dự kiến sẽ tuân theo đường cong logistic \(R = R\left( x \right) = \frac{{5000}}{{1 + 5{e^{ – x}}}},x \ge 0\), trong đó thời gian \(x\) được tính bằng năm. Hỏi tốc độ bán hàng đạt tối đa vào năm nào?
Hướng dẫn:
+ Tìm công thức \(R’\left( x \right)\).
+ Tìm \(x\) để \(R’\left( x \right)\) đạt giá trị lớn nhất.
Lời giải:
Hàm biểu thị tốc độ bán hàng là \(R’\left( x \right) = \frac{{25000{e^{ – x}}}}{{{{\left( {1 + 5{e^{ – x}}} \right)}^2}}},{\rm{ x}} \ge 0\).
Tốc độ bán hàng tối đa khi \(R’\left( x \right)\) đạt giá trị lớn nhất, ta cần tìm giá trị lớn nhất của \(R’\left( x \right)\) trên \(\left[ {0; + \infty } \right)\).
Ta có \(R”\left( x \right) = – 25000 \cdot \frac{{{e^{ – x}}{{\left( {1 + 5{e^{ – x}}} \right)}^2} + {e^{ – x}} \cdot 2\left( {1 + 5{e^{ – x}}} \right) \cdot 5{e^{ – x}}}}{{{{\left( {1 + 5{e^{ – x}}} \right)}^4}}} = \frac{{25000\left( {5{e^{ – x}} – 1} \right)}}{{{{\left( {1 + 5{e^{ – x}}} \right)}^3}}}\)
Khi đó \(R”\left( x \right) = 0 \Leftrightarrow \frac{{25000\left( {5{e^{ – x}} – 1} \right)}}{{{{\left( {1 + 5{e^{ – x}}} \right)}^3}}} = 0 \Leftrightarrow \left( {5{e^{ – x}} – 1} \right) = 0 \Leftrightarrow x = \ln 5\).
Lập bảng biến thiên
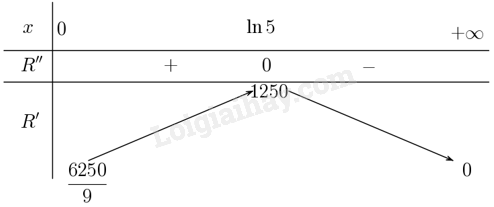
Từ bảng biến thiên suy ra \(R’\) đạt giá trị lớn nhất tại \(x = \ln 5 \approx 1,61\). Vậy tốc độ bán hàng đạt tối đa vào thời điểm năm thứ hai.