Để chứng minh rằng hai điểm \(M\) và \(M’\) đối xứng với nhau qua \(I\), ta chứng minh \(I\) là trung điểm của \(MM’\). Vận dụng kiến thức giải Giải bài 6 trang 32 sách bài tập toán 12 – Chân trời sáng tạo – Bài 4. Khảo sát và vẽ đồ thị một số hàm cơ bản. Ta đã biết đồ thị hàm số \(y = \frac{{2{\rm{x}} – 1}}{{x + 1}}\…
Đề bài/câu hỏi:
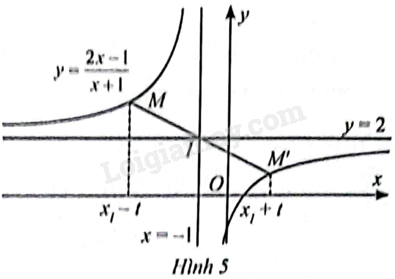
Ta đã biết đồ thị hàm số \(y = \frac{{2{\rm{x}} – 1}}{{x + 1}}\) có tiệm cận đứng là đường thẳng \(x = – 1\) và tiệm cận ngang là đường thẳng \(y = 2\).
a) Tìm toạ độ giao điểm \(I\) của đường tiệm cận.
b) Với \(t\) tuỳ ý \(\left( {t \ne 0} \right)\), gọi \(M\) và \(M’\) lần lượt là hai điểm trên đồ thị hàm số có hoành độ lần lượt là \({x_M} = {x_I} – t\) và \({x_{M’}} = {x_I} + t\). Tìm các tung độ \(y\left( {{x_M}} \right)\) và \(y\left( {{x_{M’}}} \right)\).
Từ đó, chứng minh rằng hai điểm \(M\) và \(M’\) đối xứng với nhau qua \(I\).
Hướng dẫn:
Để chứng minh rằng hai điểm \(M\) và \(M’\) đối xứng với nhau qua \(I\), ta chứng minh \(I\) là trung điểm của \(MM’\).
Lời giải:
a) Đồ thị hàm số \(y = \frac{{2{\rm{x}} – 1}}{{x + 1}}\) có tiệm cận đứng là đường thẳng \(x = – 1\) và tiệm cận ngang là đường thẳng \(y = 2\) nên giao điểm của hai đường tiệm cận là \(I\left( { – 1;2} \right)\).
b) Ta có: \({x_M} = {x_I} – t = – 1 – t \Rightarrow {y_M} = \frac{{2{{\rm{x}}_M} – 1}}{{{x_M} + 1}} = \frac{{2\left( { – 1 – t} \right) – 1}}{{\left( { – 1 – t} \right) + 1}} = \frac{{2t + 3}}{t}\)
\({x_{M’}} = {x_I} + t = – 1 + t \Rightarrow {y_{M’}} = \frac{{2{{\rm{x}}_{M’}} – 1}}{{{x_{M’}} + 1}} = \frac{{2\left( { – 1 + t} \right) – 1}}{{\left( { – 1 + t} \right) + 1}} = \frac{{2t – 3}}{t}\)
Vì :
\(\begin{array}{l}{x_M} + {x_{M’}} = \left( {{x_I} – t} \right) + \left( {{x_I} + t} \right) = 2{x_I};\\{y_M} + {y_{M’}} = \frac{{2t + 3}}{t} + \frac{{2t – 3}}{t} = \frac{{\left( {2t + 3} \right) + \left( {2t – 3} \right)}}{t} = 4 = 2{y_I}\end{array}\)
nên \(I\) là trung điểm của \(MM’\).
Vậy hai điểm \(M\) và \(M’\) đối xứng với nhau qua \(I\).