‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} – {a_1}\). Gợi ý giải Giải bài 5 trang 105 sách bài tập toán 12 – Chân trời sáng tạo – Bài 2. Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm. Bảng dưới đây thống kê cân nặng của một số quả cam canh được thu hoạch từ một vườn cam…
Đề bài/câu hỏi:
Bảng dưới đây thống kê cân nặng của một số quả cam canh được thu hoạch từ một vườn cam vào năm 2022 và năm 2023
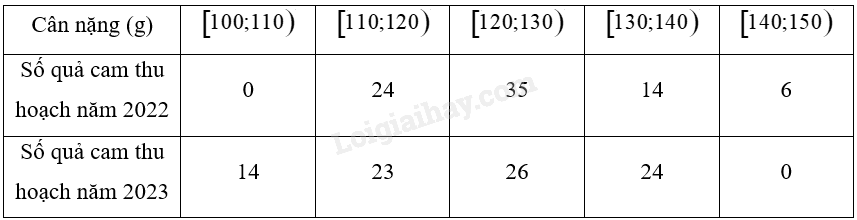
Hãy so sánh độ đồng đều của cân nặng các trái cam thu hoạch trong hai năm trên
a) theo khoảng biến thiên;
b) theo khoảng tứ phân vị;
c) theo phương sai.
Hướng dẫn:
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} – {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
Tứ phân vị thứ \(k\) được xác định như sau: \({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} – C}}{{{n_m}}}\left( {{u_{m + 1}} – {u_m}} \right)\)
trong đó:
• \(n = {n_1} + {n_2} + … + {n_k}\) là cỡ mẫu;
• \(\left[ {{u_m};{u_{m + 1}}} \right)\) là nhóm chứa tứ phân vị thứ \(k\);
• \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ \(k\);
• \(C = {n_1} + {n_2} + … + {n_{m – 1}}\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} – {Q_1}\).
‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\(\begin{array}{l}{S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} – \overline x } \right)}^2} + {n_2}{{\left( {{c_2} – \overline x } \right)}^2} + … + {n_k}{{\left( {{c_k} – \overline x } \right)}^2}} \right]\\ & = \frac{1}{n}\left[ {{n_1}c_1^2 + {n_2}c_2^2 + … + {n_k}c_k^2} \right] – {\overline x ^2}\end{array}\)
Lời giải:
a) Khoảng biến thiên của cân nặng của các trái cam thu hoạch năm 2022 là:
\({R_A} = 150 – 110 = 40\) (g).
Khoảng biến thiên của cân nặng của các trái cam thu hoạch năm 2023 là:
\({R_B} = 140 – 100 = 40\) (g).
Do đó, nếu so sánh theo khoảng biến thiên thì độ đồng đều của cân nặng các trái cam thu hoạch trong hai năm bằng nhau.
b) • Tứ phân vị của cân nặng của các trái cam thu hoạch năm 2022:
\({n_A} = 24 + 35 + 14 + 6 = 79\)
Gọi \({x_1};{x_2};…;{x_{79}}\) là mẫu số liệu gốc gồm cân nặng của 79 trái cam thu hoạch năm 2022 theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{20}} + {x_{21}}} \right) \in \left[ {110;120} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_{A1}} = 110 + \frac{{\frac{{1.79}}{4} – 0}}{{24}}\left( {120 – 110} \right) = \frac{{5675}}{{48}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{59}} + {x_{60}}} \right) \in \left[ {130;140} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_{A3}} = 130 + \frac{{\frac{{3.79}}{4} – \left( {24 + 35} \right)}}{{14}}\left( {140 – 130} \right) = \frac{{3645}}{{28}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
\(\Delta {Q_A} = {Q_{A3}} – {Q_{A1}} = \frac{{3645}}{{28}} – \frac{{5675}}{{48}} = \frac{{4015}}{{336}} \approx 11,95\) (g).
• Tứ phân vị của cân nặng của các trái cam thu hoạch năm 2023:
\({n_B} = 14 + 23 + 26 + 24 = 87\)
Gọi \({x_1};{x_2};…;{x_{87}}\) là mẫu số liệu gốc gồm cân nặng của 87 trái cam thu hoạch năm 2023 theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{22}} + {x_{23}}} \right) \in \left[ {110;120} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_{B1}} = 110 + \frac{{\frac{{1.87}}{4} – 14}}{{23}}\left( {120 – 110} \right) = \frac{{5215}}{{46}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{65}} + {x_{66}}} \right) \in \left[ {130;140} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_{B3}} = 130 + \frac{{\frac{{3.87}}{4} – \left( {14 + 23 + 26} \right)}}{{24}}\left( {140 – 130} \right) = \frac{{2095}}{{16}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
\(\Delta {Q_B} = {Q_{B3}} – {Q_{B1}} = \frac{{2095}}{{16}} – \frac{{5215}}{{46}} = \frac{{6465}}{{368}} \approx 17,57\) (g).
Do đó, nếu so sánh theo khoảng tứ phân vị thì cân nặng các trái cam thu hoạch trong năm 2022 đồng đều hơn cân nặng các trái cam thu hoạch trong năm 2023.
c) Ta có bảng sau:
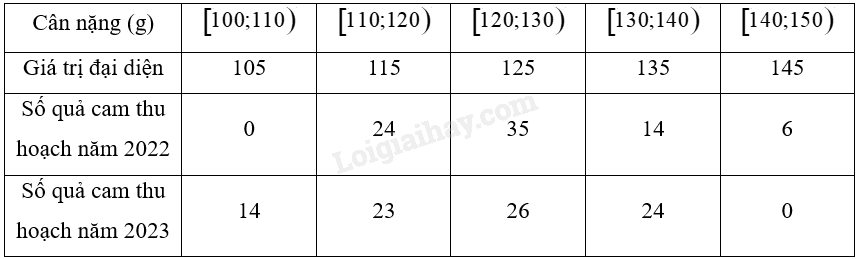
• Phương sai của cân nặng của các trái cam thu hoạch năm 2022:
Cỡ mẫu \({n_A} = 79\)
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline {{x_A}} = \frac{{24.115 + 35.125 + 14.135 + 6.145}}{{79}} = \frac{{9895}}{{79}}\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\(S_A^2 = \frac{1}{{79}}\left( {{{24.115}^2} + {{35.125}^2} + {{14.135}^2} + {{6.145}^2}} \right) – {\frac{{9895}}{{79}}^2} \approx 78,41\)
• Phương sai của cân nặng của các trái cam thu hoạch năm 2023:
Cỡ mẫu \({n_B} = 87\)
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline {{x_B}} = \frac{{14.105 + 23.115 + 26.125 + 24.135}}{{87}} = \frac{{3535}}{{29}}\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\(S_B^2 = \frac{1}{{87}}\left( {{{14.105}^2} + {{23.115}^2} + {{16.125}^2} + {{24.135}^2}} \right) – {\left( {\frac{{3535}}{{29}}} \right)^2} \approx 108,76\)
Do \(S_A^2 < S_B^2\) nên khi so sánh theo phương sai thì cân nặng các trái cam thu hoạch trong năm 2022 đồng đều hơn cân nặng các trái cam thu hoạch trong năm 2023.