‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} – {a_1}\). Phân tích, đưa ra lời giải Giải bài 4 trang 110 sách bài tập toán 12 – Chân trời sáng tạo – Bài tập cuối chương 3. Một nhóm nghiên cứu đã đo mức độ ồn của các phương tiến giao thông trên hai đường phố vào…
Đề bài/câu hỏi:
Một nhóm nghiên cứu đã đo mức độ ồn của các phương tiến giao thông trên hai đường phố vào một ngày trong tuần, trong khoảng thời gian từ 5 giờ 30 phút đến 10 giờ 10 phút. Người ta thực đã thực hiện 92 lần đo ở mỗi con đường vào những khoảng thời gian như nhau. Kết quả thống kê được ghi lại như trong bảng sau:
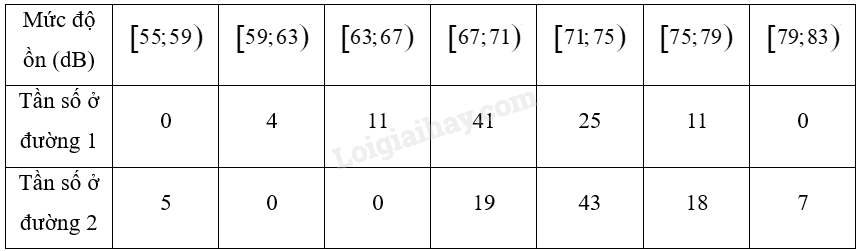
Hãy so sánh độ phân tán mức độ ồn của các phương tiện giao thông ở hai đường phố trên:
a) theo khoảng biến thiên;
b) theo khoảng tứ phân vị;
c) theo phương sai.
Hướng dẫn:
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} – {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
Tứ phân vị thứ \(k\) được xác định như sau: \({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} – C}}{{{n_m}}}\left( {{u_{m + 1}} – {u_m}} \right)\)
trong đó:
• \(n = {n_1} + {n_2} + … + {n_k}\) là cỡ mẫu;
• \(\left[ {{u_m};{u_{m + 1}}} \right)\) là nhóm chứa tứ phân vị thứ \(k\);
• \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ \(k\);
• \(C = {n_1} + {n_2} + … + {n_{m – 1}}\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} – {Q_1}\).
‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\(\begin{array}{l}{S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} – \overline x } \right)}^2} + {n_2}{{\left( {{c_2} – \overline x } \right)}^2} + … + {n_k}{{\left( {{c_k} – \overline x } \right)}^2}} \right]\\ & = \frac{1}{n}\left[ {{n_1}c_1^2 + {n_2}c_2^2 + … + {n_k}c_k^2} \right] – {\overline x ^2}\end{array}\)
Lời giải:
Ta có bảng sau:
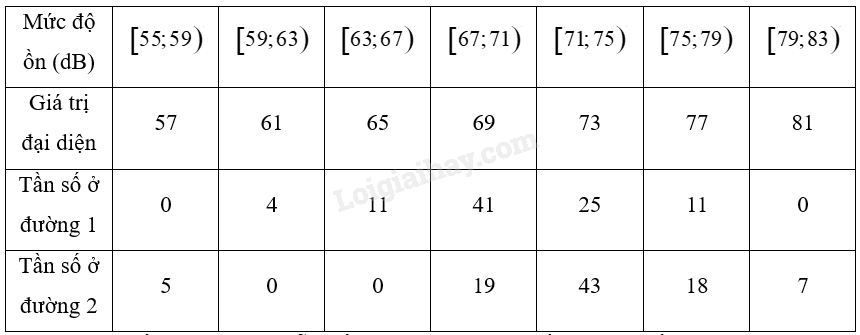
a) Khoảng biến thiên của mẫu số liệu ghép nhóm về mức độ ồn trên đường I là: \({R_I} = 79 – 59 = 20\left( {dB} \right)\).
Khoảng biến thiên của mẫu số liệu ghép nhóm về mức độ ồn trên đường II là: \({R_{II}} = 83 – 55 = 28\left( {dB} \right)\).
Do đó, nếu so sánh theo khoảng biến thiên, mức độ ồn trên đường II phân tán hơn trên đường I.
b) • Tứ phân vị của mẫu số liệu ghép nhóm về mức độ ồn trên đường I:
Cỡ mẫu: \({n_I} = 4 + 11 + 41 + 25 + 11 = 92\)
Gọi \({x_1};{x_2};…;{x_{92}}\) là mẫu số liệu gốc gồm mức độ ồn trên đường I theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{23}} + {x_{24}}} \right) \in \left[ {67;71} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_{I1}} = 67 + \frac{{\frac{{1.92}}{4} – \left( {4 + 11} \right)}}{{41}}\left( {71 – 67} \right) = \frac{{2779}}{{41}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{69}} + {x_{71}}} \right) \in \left[ {71;75} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_{I3}} = 71 + \frac{{\frac{{3.92}}{4} – \left( {4 + 11 + 41} \right)}}{{25}}\left( {75 – 71} \right) = \frac{{1827}}{{25}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
\(\Delta {Q_I} = {Q_{I3}} – {Q_{I3}} = \frac{{1827}}{{25}} – \frac{{2779}}{{41}} = \frac{{5432}}{{1025}} \approx 5,3\left( {dB} \right)\).
• Tứ phân vị của mẫu số liệu ghép nhóm về mức độ ồn trên đường II:
Cỡ mẫu: \({n_{II}} = 5 + 19 + 43 + 18 + 7 = 92\)
Gọi \({x_1};{x_2};…;{x_{92}}\) là mẫu số liệu gốc gồm mức độ ồn trên đường II theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{23}} + {x_{24}}} \right) \in \left[ {67;71} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_{II1}} = 67 + \frac{{\frac{{1.92}}{4} – 5}}{{19}}\left( {71 – 67} \right) = \frac{{1345}}{{19}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{69}} + {x_{71}}} \right) \in \left[ {75;79} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_{II3}} = 75 + \frac{{\frac{{3.92}}{4} – \left( {5 + 19 + 43} \right)}}{{18}}\left( {75 – 71} \right) = \frac{{679}}{9}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
\(\Delta {Q_{II}} = {Q_{II3}} – {Q_{II3}} = \frac{{679}}{9} – \frac{{1345}}{{19}} = \frac{{796}}{{171}} \approx 4,65\left( {dB} \right)\).
Do đó, nếu so sánh theo khoảng tứ phân vị, mức độ ồn trên đường I phân tán hơn trên đường II.
c) • Phương sai của mẫu số liệu ghép nhóm về mức độ ồn trên đường I:
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline {{x_I}} = \frac{{4.61 + 11.65 + 41.69 + 25.73 + 11.77}}{{92}} = \frac{{1615}}{{23}}\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\(S_I^2 = \frac{1}{{92}}\left( {{{4.61}^2} + {{11.65}^2} + {{41.69}^2} + {{25.73}^2} + {{11.77}^2}} \right) – {\left( {\frac{{1615}}{{23}}} \right)^2} = \frac{{8048}}{{529}} \approx 15,21\)
• Phương sai của mẫu số liệu ghép nhóm về mức độ ồn trên đường II:
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline {{x_{II}}} = \frac{{5.57 + 19.69 + 43.73 + 18.77 + 7.81}}{{92}} = \frac{{1672}}{{23}}\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\(S_{II}^2 = \frac{1}{{92}}\left( {{{5.57}^2} + {{19.69}^2} + {{43.73}^2} + {{18.77}^2} + {{7.81}^2}} \right) – {\left( {\frac{{1672}}{{23}}} \right)^2} \approx 25,12\)
Do \(S_I^2 < S_{II}^2\) nên khi so sánh theo phương sai, mức độ ồn trên đường II phân tán hơn trên đường I.