• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\): Bước 1. Phân tích, đưa ra lời giải Giải bài 2 trang 17 sách bài tập toán 12 – Chân trời sáng tạo – Bài 2. Giá trị lớn nhất – giá trị nhỏ nhất của hàm số. Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:…
Đề bài/câu hỏi:
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x^3} – 8{x^2} – 12x + 1\) trên đoạn \(\left[ { – 2;9} \right]\);
b) \(y = – 2{x^3} + 9{x^2} – 17\) trên nửa khoảng \(\left( { – \infty ;4} \right]\);
c) \(y = {x^3} – 12x + 4\) trên đoạn \(\left[ { – 6;3} \right]\);
d) \(y = 2{x^3} – {x^2} – 28x – 3\) trên đoạn \(\left[ { – 2;1} \right]\);
e) \(y = – 3{x^3} + 4{x^2} – 5x – 17\) trên đoạn \(\left[ { – 1;2} \right]\).
Hướng dẫn:
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\):
Bước 1. Tìm các điểm \({x_1},{x_2},…,{x_n}\) thuộc khoảng \(\left( {a;b} \right)\) mà tại đó \(f’\left( x \right)\) bằng 0 hoặc không tồn tại.
Bước 2. Tính \(f\left( a \right);f\left( {{x_1}} \right);f\left( {{x_2}} \right);…;f\left( {{x_n}} \right);f\left( b \right)\).
Bước 3. Gọi \(M\) là số lớn nhất và \(m\) là số nhỏ nhất trong các giá trị tìm được ở Bước 2. Khi đó: \(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\).
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải:
a) Xét hàm số \(y = f\left( x \right) = {x^3} – 8{x^2} – 12x + 1\) trên đoạn \(\left[ { – 2;9} \right]\).
Ta có: \(f’\left( x \right) = 3{{\rm{x}}^2} – 16{\rm{x}} – 12\)
\(f’\left( x \right) = 0 \Leftrightarrow x = 6\) hoặc \(x = – \frac{2}{3}\).
\(f\left( { – 2} \right) = – 15;f\left( { – \frac{2}{3}} \right) = \frac{{139}}{{27}};f\left( 6 \right) = – 143;f\left( 9 \right) = – 26\)
Vậy \(\mathop {\max }\limits_{\left[ { – 2;9} \right]} f\left( x \right) = f\left( { – \frac{2}{3}} \right) = \frac{{139}}{{27}},\mathop {\min }\limits_{\left[ { – 2;9} \right]} f\left( x \right) = f\left( 6 \right) = – 143\).
b) Xét hàm số \(y = f\left( x \right) = – 2{x^3} + 9{x^2} – 17\) trên nửa khoảng \(\left( { – \infty ;4} \right]\).
Ta có: \(f’\left( x \right) = – 6{{\rm{x}}^2} + 18{\rm{x}}\)
\(f’\left( x \right) = 0 \Leftrightarrow x = 0\) hoặc \(x = 3\).
Bảng biến thiên của hàm số trên nửa khoảng \(\left( { – \infty ;4} \right]\):
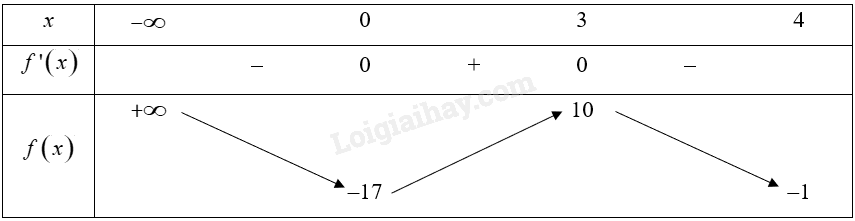
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( { – \infty ;4} \right]} f\left( x \right) = f\left( 0 \right) = – 17\), hàm số không có giá trị lớn nhất trên nửa khoảng \(\left( { – \infty ;4} \right]\).
c) Xét hàm số \(y = f\left( x \right) = {x^3} – 12x + 4\) trên đoạn \(\left[ { – 6;3} \right]\).
Ta có: \(f’\left( x \right) = 3{{\rm{x}}^2} – 12\)
\(f’\left( x \right) = 0 \Leftrightarrow x = 2\) hoặc \(x = – 2\).
\(f\left( { – 6} \right) = – 140;f\left( { – 2} \right) = 20;f\left( 2 \right) = – 12;f\left( 3 \right) = – 5\)
Vậy \(\mathop {\max }\limits_{\left[ { – 6;3} \right]} f\left( x \right) = f\left( { – 2} \right) = 20,\mathop {\min }\limits_{\left[ { – 6;3} \right]} f\left( x \right) = f\left( { – 6} \right) = – 140\).
d) Xét hàm số \(y = 2{x^3} – {x^2} – 28x – 3\) trên đoạn \(\left[ { – 2;1} \right]\).
Ta có: \(f’\left( x \right) = 6{{\rm{x}}^2} – 2{\rm{x}} – 28\)
\(f’\left( x \right) = 0 \Leftrightarrow x = \frac{7}{3}\) (loại) hoặc \(x = – 2\).
\(f\left( { – 2} \right) = 33;f\left( 1 \right) = – 30\)
Vậy \(\mathop {\max }\limits_{\left[ { – 2;1} \right]} f\left( x \right) = f\left( { – 2} \right) = 33,\mathop {\min }\limits_{\left[ { – 2;1} \right]} f\left( x \right) = f\left( 1 \right) = – 30\).
e) Xét hàm số \(y = f\left( x \right) = – 3{x^3} + 4{x^2} – 5x – 17\) trên đoạn \(\left[ { – 1;2} \right]\).
Ta có: \(f’\left( x \right) = – 9{{\rm{x}}^2} + 8{\rm{x}} – 5 = – 9{\left( {x – \frac{4}{9}} \right)^2} – \frac{{29}}{9} < 0,\forall x \in \left[ { – 1;2} \right]\)
\(f\left( { – 1} \right) = – 5;f\left( 2 \right) = – 35\)
Vậy \(\mathop {\max }\limits_{\left[ { – 1;2} \right]} f\left( x \right) = f\left( { – 1} \right) = – 5,\mathop {\min }\limits_{\left[ { – 1;2} \right]} f\left( x \right) = f\left( 2 \right) = – 35\).