‒ Sử dụng quy tắc cộng, quy tắc hình hộp. ‒ Sử dụng tích vô hướng của hai vectơ: \(\cos \left( {\overrightarrow a . Hướng dẫn trả lời Giải bài 16 trang 78 sách bài tập toán 12 – Chân trời sáng tạo – Bài tập cuối chương 2. Chọn đúng hoặc sai cho mỗi ý a, b, c, d. Cho hình lập phương (ABCD.A’B’C’D’) có cạnh bằng 2….
Đề bài/câu hỏi:
Chọn đúng hoặc sai cho mỗi ý a, b, c, d.Cho hình lập phương \(ABCD.A’B’C’D’\) có cạnh bằng 2. a) \(\overrightarrow {AB} = \overrightarrow {C’D’} \). b) \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {D’C’} \). c) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} = \overrightarrow {AC’} \). d) \(\overrightarrow {AC} .\overrightarrow {AD’} = 8\).
Hướng dẫn:
‒ Sử dụng quy tắc cộng, quy tắc hình hộp.
‒ Sử dụng tích vô hướng của hai vectơ: \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\).
Lời giải:
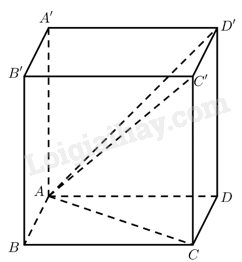
\(ABC’D’\) là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {D’C’} \). Vậy a) sai.
\(ABCD\) là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \).
Do đó \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {DC} = 2\overrightarrow {D’C’} \). Vậy b) đúng.
Theo quy tắc hình hộp ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} = \overrightarrow {AC’} \). Vậy c) đúng.
Xét tam giác \(AC{\rm{D}}’\) có \(AC,A{\rm{D}}’,C{\rm{D}}’\) đều là các đường chéo hình vuông. Do đó \(AC = A{\rm{D}}’ = C{\rm{D}}’ = AB\sqrt 2 = 2\sqrt 2 \).
Vậy tam giác \(AC{\rm{D}}’\) là tam giác đều. Suy ra \(\widehat {CAD’} = {60^ \circ }\)
\(\overrightarrow {AC} .\overrightarrow {AD’} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AD’} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {AD’} } \right) = AC.AD’.\cos \widehat {CAD’} = 2\sqrt 2 .2\sqrt 2 .\cos {60^ \circ } = 4\).
Vậy d) sai.
a) S.
b) Đ.
c) Đ.
d) S.