Sử dụng công thức tính diện tích hình thang để tính diện tích \(S\left( x \right)\). Hướng dẫn cách giải/trả lời Giải bài 10 trang 18 sách bài tập toán 12 – Chân trời sáng tạo – Bài 2. Giá trị lớn nhất – giá trị nhỏ nhất của hàm số. Cho hình thang cân có đáy nhỏ và hai cạnh bên bằng nhau và bằng 5….
Đề bài/câu hỏi:
Cho hình thang cân có đáy nhỏ và hai cạnh bên bằng nhau và bằng 5. Tìm diện tích lớn nhất của hình thang cân đó.
Hướng dẫn:
Sử dụng công thức tính diện tích hình thang để tính diện tích \(S\left( x \right)\), sau đó tìm giá trị lớn nhất của hàm số \(S\left( x \right)\).
Lời giải:
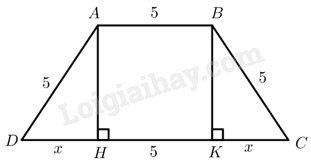
Xét hình thang cân \(ABCD\) có đáy nhỏ \(AB\), gọi \(H,K\) lần lượt là chân đường cao kẻ từ \(A\) và \(B\) xuống \(CD\).
Ta có:
\(C{\rm{D}} = 5 + 2{\rm{x}},AH = \sqrt {A{{\rm{D}}^2} – D{H^2}} = \sqrt {{5^2} – {x^2}} = \sqrt {25 – {x^2}} \)
Diện tích hình thang là:
\(S = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).AH = \frac{1}{2}\left( {5 + 5 + 2{\rm{x}}} \right).\sqrt {25 – {x^2}} = \left( {5 + {\rm{x}}} \right).\sqrt {25 – {x^2}} \)
Do \(DH < AD\) nên \({\rm{x}} < 5\).
Xét hàm số \(S\left( x \right) = \left( {5 + {\rm{x}}} \right).\sqrt {25 – {x^2}} \) trên nửa khoảng \(\left[ {0;5} \right)\).
Ta có:
\(S’\left( x \right) = {\left( {5 + {\rm{x}}} \right)^\prime }.\sqrt {25 – {x^2}} + \left( {5 + {\rm{x}}} \right).{\left( {\sqrt {25 – {x^2}} } \right)^\prime } = \sqrt {25 – {x^2}} + \left( {5 + {\rm{x}}} \right).\frac{{ – {\rm{x}}}}{{\sqrt {25 – {x^2}} }} = \frac{{ – 2{{\rm{x}}^2} – 5x + 25}}{{\sqrt {25 – {x^2}} }}\)
\(S’\left( x \right) = 0 \Leftrightarrow x = \frac{5}{2}\) hoặc \(x = – 5\) (loại)
Bảng biến thiên của hàm số trên nửa khoảng \(\left[ {0;5} \right)\):
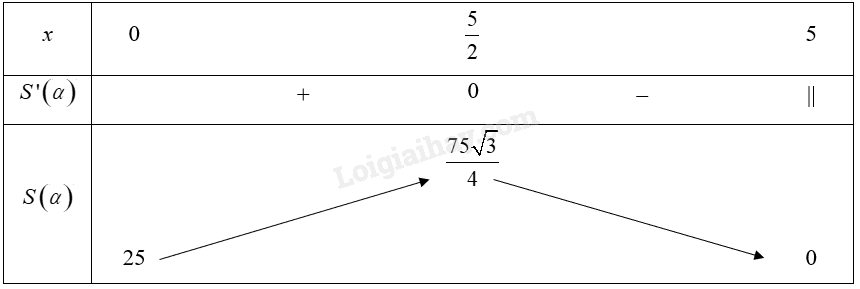
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_{\left[ {0;5} \right)} S\left( x \right) = S\left( {\frac{5}{2}} \right) = \frac{{75\sqrt 3 }}{4}\).
Vậy hình thang cân \(ABCD\) có diện tích lớn nhất bằng \(\frac{{75\sqrt 3 }}{4}\).