Dựa vào đồ thị hàm số. Phân tích và giải Giải bài 1 trang 10 sách bài tập toán 12 – Chân trời sáng tạo – Bài 1. Tính đơn điệu và cực trị của hàm số. Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 3….
Đề bài/câu hỏi:
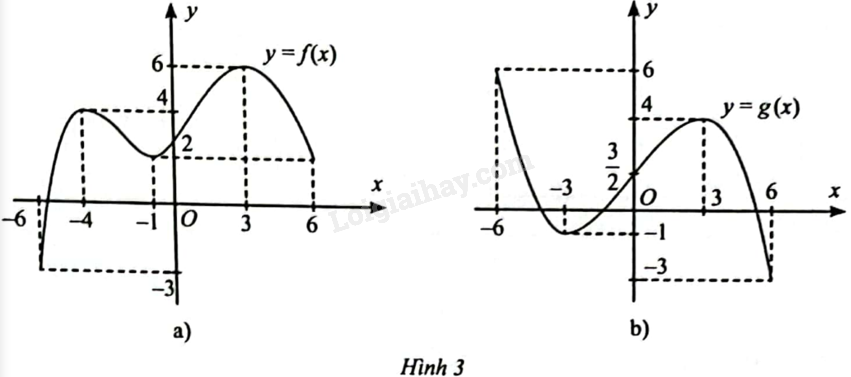
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 3.
Hướng dẫn:
Dựa vào đồ thị hàm số.
Lời giải:
Hình 3a: Hàm số \(y = f\left( x \right)\) đồng biến trên các khoảng \(\left( { – 6; – 4} \right)\) và \(\left( { – 1;3} \right)\), nghịch biến trên các khoảng \(\left( { – 4; – 1} \right)\) và \(\left( {3;6} \right)\).
Hàm số \(y = f\left( x \right)\) có:
• \(x = – 1\) là điểm cực tiểu vì \(f\left( x \right) > f\left( { – 1} \right)\) với mọi \(x \in \left( { – 4;0} \right)\backslash \left\{ { – 1} \right\},{y_{CT}} = f\left( { – 1} \right) = 2\).
• \(x = 3\) là điểm cực đại vì \(f\left( x \right) < f\left( 3 \right)\) với mọi $x\in \left( 0;6 \right)\backslash \left\{ 3 \right\}, {{y}_{CĐ}}=f\left( 3 \right)=6$.
Hình 3b: Hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( { – 3;3} \right)\), nghịch biến trên các khoảng \(\left( { – 6; – 3} \right)\) và \(\left( {3;6} \right)\).
Hàm số \(y = g\left( x \right)\) có:
• \(x = – 3\) là điểm cực tiểu vì \(g\left( x \right) > g\left( { – 3} \right)\) với mọi \(x \in \left( { – 6;0} \right)\backslash \left\{ { – 3} \right\},{y_{CT}} = g\left( { – 3} \right) = – 1\).
• \(x = 3\) là điểm cực đại vì \(g\left( x \right) < g\left( 3 \right)\) với mọi $x\in \left( 0;6 \right)\backslash \left\{ 3 \right\},{{y}_{CĐ}}=g\left( 3 \right)=4$.