Các bước để tìm khoảng đồng biến, nghịch biến của hàm số \(f\left( x \right)\): Bước 1. Phân tích và giải Giải bài 84 trang 39 sách bài tập toán 12 – Cánh diều – Bài tập cuối chương 1. Kết luận nào sau đây là đúng đối với hàm số \(y = {\left( {\frac{1}{2}} \right)^{{x^2}}}\)? A….
Đề bài/câu hỏi:
Kết luận nào sau đây là đúng đối với hàm số \(y = {\left( {\frac{1}{2}} \right)^{{x^2}}}\)?
A. Hàm số đồng biến trên \(\mathbb{R}\).
B. Hàm số nghịch biến trên \(\mathbb{R}\).
C. Hàm số đồng biến trên khoảng \(\left( { – \infty ;0} \right)\) và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
D. Hàm số nghịch biến trên khoảng \(\left( { – \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
Hướng dẫn:
Các bước để tìm khoảng đồng biến, nghịch biến của hàm số \(f\left( x \right)\):
Bước 1. Tìm tập xác định của hàm số \(y = f\left( x \right)\).
Bước 2. Tính đạo hàm \(f’\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,…,n} \right)\) mà tại đó hàm số có đạo hàm bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên.
Bước 4. Căn cứ vào bảng biến thiên, nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
Hàm số có tập xác định là \(\mathbb{R}\).
Ta có:
\({y^\prime } = {\left( {{x^2}} \right)^\prime }.{\left( {\frac{1}{2}} \right)^{{x^2}}}.\ln \frac{1}{2} = – 2{\rm{x}}{\rm{.}}{\left( {\frac{1}{2}} \right)^{{x^2}}}.\ln 2\)
\(y’ = 0\) khi \(x = 0\).
Bảng biến thiên của hàm số:
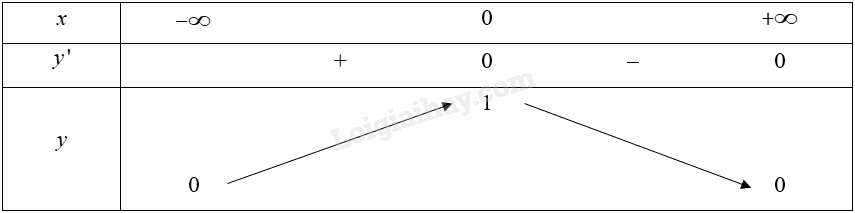
Vậy hàm số đồng biến trên khoảng \(\left( { – \infty ;0} \right)\); nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
Chọn C.