Xét đồ thị hàm số. Hướng dẫn cách giải/trả lời Giải bài 78 trang 37 sách bài tập toán 12 – Cánh diều – Bài 4. Khảo sát sự biến thiên và vẽ đồ thị hàm số. Cho hàm số bậc ba (y = fleft( x right) = a{x^3} + b{x^2} + cx + d) có đồ…
Đề bài/câu hỏi:
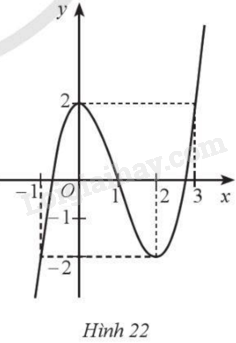
Cho hàm số bậc ba \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị là đường cong như Hình 22. Căn cứ vào đồ thị hàm số:
a) Tìm khoảng đơn điệu, điểm cực đại, cực tiểu của hàm số.
b) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { – 1;2} \right]\)
c) Tìm điểm trên đồ thị hàm số có hoành độ bằng 2.
d) Tìm điểm trên đồ thị hàm số có tung độ bằng 2.
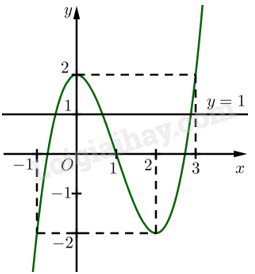
e) Đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại mấy điểm?
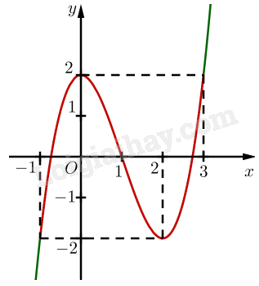
g) Với giá trị nào của \(x\) thì \( – 2 < f\left( x \right) < 2\)?
h) Tìm công thức xác định hàm số \(f\left( x \right)\).
Hướng dẫn:
Xét đồ thị hàm số.
Lời giải:
a) Dựa vào đồ thị hàm số, ta có:
‒ Hàm số đồng biến trên các khoảng \(\left( { – \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\); nghịch biến trên khoảng \(\left( {0;2} \right)\).
‒ Hàm số đạt cực đại tại điểm \(x = 0\), đạt cực tiểu tại điểm \(x = 2\).
b) Trên đoạn \(\left[ { – 1;2} \right]\), hàm số đạt giá trị lớn nhất bằng 2 tại \(x = 0\), đạt giá trị nhỏ nhất bằng ‒2 tại \(x = – 1,x = 2\).
c) Điểm trên đồ thị hàm số có hoành độ bằng 2 là \(\left( {2; – 2} \right)\).
d) Điểm trên đồ thị hàm số có tung độ bằng 2 là \(\left( {0;2} \right)\) và \(\left( {3;2} \right)\).
e) Đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm.
g) Dựa vào đồ thị hàm số, ta có: \( – 2 < f\left( x \right) < 2,\forall x \in \left( { – 1;3} \right)\backslash \left\{ {0;2} \right\}\) (phần màu đỏ).
h) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2. Vậy \(d = 2\).
Đồ thị hàm số đi qua điểm \(\left( {1;0} \right)\) nên ta có: \(a{.1^3} + b{.1^2} + c.1 + 2 = 0 \Leftrightarrow a + b + c = – 2\).
Đồ thị hàm số đi qua điểm \(\left( { – 1; – 2} \right)\) nên ta có: \(a.{\left( { – 1} \right)^3} + b.{\left( { – 1} \right)^2} + c.\left( { – 1} \right) + 2 = – 2\)
\( \Leftrightarrow – a + b – c = – 4\).
Đồ thị hàm số đi qua điểm \(\left( {2; – 2} \right)\) nên ta có: \(a{.2^3} + b{.2^2} + c.2 + 2 = – 2 \Leftrightarrow 8a + 4b + 2c = – 4\).
Từ đó ta có \(a = 1,b = – 3,c = 0\).
Vậy hàm số cần tìm là: \(y = f\left( x \right) = {x^3} – 3{{\rm{x}}^2} + 2\).