Dựa vào đồ thị hàm số, xác định các đường tiệm cận. Vận dụng kiến thức giải Giải bài 57 trang 25 sách bài tập toán 12 – Cánh diều – Bài 3. Đường tiệm cận của đồ thị hàm số. Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\…
Đề bài/câu hỏi:
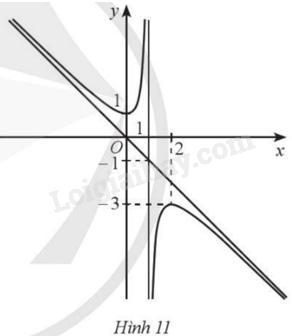
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\) và có đồ thị như Hình 11.
Các đường tiệm cận của đồ thị hàm số là:
A. Tiệm cận đứng là đường thẳng \(x = 1\) và tiệm cận xiên là đường thẳng \(y = – x\).
B. Tiệm cận đứng là đường thẳng \(x = – 1\) và tiệm cận xiên là đường thẳng \(y = x\).
C. Tiệm cận đứng là đường thẳng \(x = 1\) và tiệm cận xiên là đường thẳng \(y = x\).
D. Tiệm cận đứng là đường thẳng \(x = 1\) và tiệm cận xiên là đường thẳng \(y = – 2x\).
Hướng dẫn:
Dựa vào đồ thị hàm số, xác định các đường tiệm cận.
Lời giải:
Dựa vào đồ thị hàm số ta có \(x = 1\) là đường tiệm cận đứng.
Đường tiệm cận xiên là đường thẳng đi qua gốc toạ độ \(O\) và điểm \(A\left( {1; – 1} \right)\). Vậy đường thẳng \(y = – x\) là đường tiệm cận xiên.
Chọn A.