Xét hàm số \(C\left( t \right)\) trên nửa khoảng \(\left[ {0; + \infty } \right)\). Hướng dẫn giải Giải bài 46 trang 20 sách bài tập toán 12 – Cánh diều – Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Nồng độ \(C\) của một loại hoá chất trong máu sau \(t\…
Đề bài/câu hỏi:
Nồng độ \(C\) của một loại hoá chất trong máu sau \(t\) giờ tiêm vào cơ thể được cho bởi công thức: \(C\left( t \right) = \frac{{3t}}{{27 + {t^3}}}\) với \(t \ge 0\) (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).
Sau khoảng bao nhiêu giờ tiêm thì nồng độ của hoá chất trong máu là cao nhất?
Hướng dẫn:
Xét hàm số \(C\left( t \right)\) trên nửa khoảng \(\left[ {0; + \infty } \right)\), lập bảng biến thiên và tìm giá trị lớn nhất của hàm số.
Lời giải:
Xét hàm số \(C\left( t \right) = \frac{{3t}}{{27 + {t^3}}}\) trên nửa khoảng \(\left[ {0; + \infty } \right)\).
Ta có:
\(C’\left( t \right) = \frac{{{{\left( {3t} \right)}^\prime }.\left( {27 + {t^3}} \right) – \left( {3t} \right).{{\left( {27 + {t^3}} \right)}^\prime }}}{{{{\left( {27 + {t^3}} \right)}^2}}} = \frac{{3\left( {27 + {t^3}} \right) – \left( {3t} \right).3{t^2}}}{{{{\left( {27 + {t^3}} \right)}^2}}} = \frac{{81 – 6{{\rm{x}}^3}}}{{{{\left( {27 + {t^3}} \right)}^2}}}\)
\(C’\left( t \right) = 0\) khi \(t = \frac{{3\sqrt[3]{4}}}{2}\).
Bảng biến thiên của hàm số:
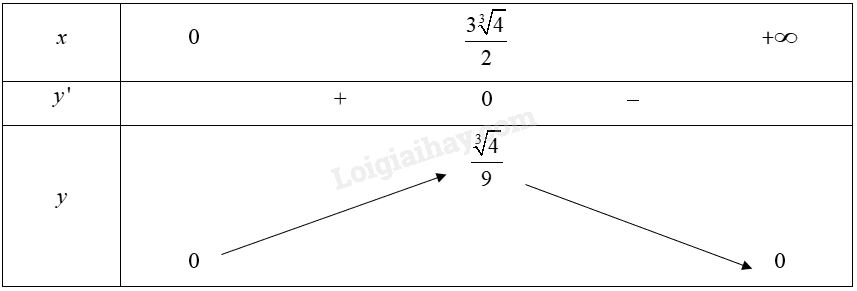
Căn cứ vào bảng biến thiên, ta có: \(\mathop {\max }\limits_{\left( {0;4} \right)} C\left( t \right) = \frac{{\sqrt[3]{4}}}{9}\) tại \(t = \frac{{3\sqrt[3]{4}}}{2}\).
Vậy sau khoảng \(t = \frac{{3\sqrt[3]{4}}}{2} \approx 2,38\) giờ thì nồng độ của hoá chất trong máu là cao nhất.