Tìm giá trị nhỏ nhất của hàm số \(S\left( x \right)\) là tổng diện tích xung quanh và diện tích đáy của thùng. Phân tích, đưa ra lời giải Giải bài 40 trang 19 sách bài tập toán 12 – Cánh diều – Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S)….
Đề bài/câu hỏi:
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S).Bác Lâm muốn gò một cái thùng bằng tôn dạng hình hộp chữ nhật không nắp có đáy là hình vuông và đựng đầy được 32 lít nước. Gọi độ dài cạnh đáy của thùng là \(x\left( {dm} \right)\), chiều cao của thùng là \(h\left( {dm} \right)\).a) Thể tích của thùng là \(V = {x^.}^2.h\left( {d{m^3}} \right)\).b) Tổng diện tích xung quanh và diện tích đáy của thùng là: \(S = 4xh + {x^2}\left( {d{m^2}} \right)\).c) Đạo hàm của hàm số \(S\left( x \right) = \frac{{128}}{x} + {x^2}\) là \(S’\left( x \right) = \frac{{128}}{{{x^2}}} + 2{\rm{x}}\).d) Để làm được cái thùng mà tốn ít nguyên liệu nhất thì độ dài cạnh đáy của thùng là 4 dm.
Hướng dẫn:
Tìm giá trị nhỏ nhất của hàm số \(S\left( x \right)\) là tổng diện tích xung quanh và diện tích đáy của thùng.
Lời giải:
Đáy của thùng là hình vuông nên diện tích đáy là \({x^2}\left( {d{m^2}} \right)\).
Vậy thể tích của thùng là \(V = {x^.}^2.h\left( {d{m^3}} \right)\). Vậy a) đúng.
Diện tích xung quanh của thùng là: \({S_{xq}} = 4{\rm{x}}h\left( {d{m^2}} \right)\).
Diện tích đáy của thùng là: .
Vậy tổng diện tích xung quanh và diện tích đáy của thùng là: \(S = 4xh + {x^2}\left( {d{m^2}} \right)\). Vậy b) đúng.
Ta có: \(S\left( x \right) = \frac{{128}}{x} + {x^2}\). Khi đó: \(S’\left( x \right) = – \frac{{128}}{{{x^2}}} + 2{\rm{x}}\). Vậy c) sai.
Thể tích của thùng là 32 lít nên ta có: \({x^.}^2.h = 32 \Leftrightarrow h = \frac{{32}}{{{x^2}}}\)
Khi đó: \(S = 4x.\frac{{32}}{{{x^2}}} + {x^2} = \frac{{128}}{x} + {x^2}\)
Xét hàm số \(S\left( x \right) = \frac{{128}}{x} + {x^2}\) trên khoảng \(\left( {0; + \infty } \right)\).
Ta có: \(S’\left( x \right) = – \frac{{128}}{{{x^2}}} + 2{\rm{x}}\)
\(S’\left( x \right) = 0\) khi \(x = 4\).
Bảng biến thiên của hàm số:
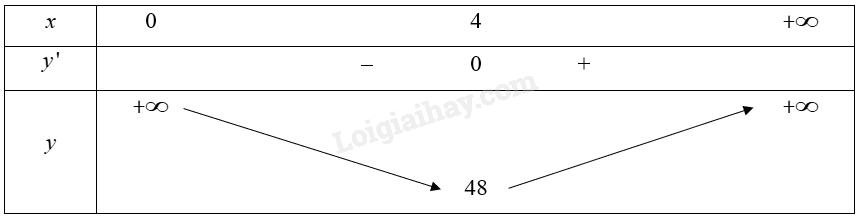
Căn cứ vào bảng biến thiên, ta có: \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} S\left( x \right) = 48\) tại \({\rm{x}} = 4\). Vậy d) đúng.
a) Đ.
b) Đ.
c) S.
d) Đ.