Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng, đoạn hay nửa khoảng bằng đạo hàm. Hướng dẫn giải Giải bài 26 trang 17 sách bài tập toán 12 – Cánh diều – Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số. Giá trị nhỏ nhất của hàm số (y = sqrt {{x^2} + 4} ) bằng: A. 2. B. 4. C….
Đề bài/câu hỏi:
Giá trị nhỏ nhất của hàm số \(y = \sqrt {{x^2} + 4} \) bằng:
A. 2.
B. 4.
C. 0.
D. 1.
Hướng dẫn:
Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng, đoạn hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải:
Hàm số có tập xác định là \(\mathbb{R}\).
Ta có: \({y^\prime } = \frac{{{{\left( {{x^2} + 4} \right)}^\prime }}}{{2\sqrt {{x^2} + 4} }} = \frac{{2{\rm{x}}}}{{2\sqrt {{x^2} + 4} }} = \frac{{\rm{x}}}{{\sqrt {{x^2} + 4} }}\)
\(y’ = 0\) khi \(x = 0\).
Bảng biến thiên của hàm số:
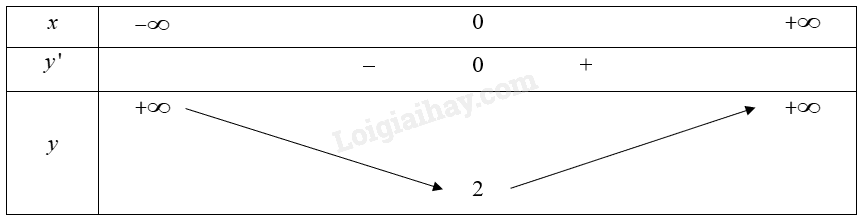
Căn cứ vào bảng biến thiên, ta có: \(\min f\left( x \right) = 2\) tại \({\rm{x}} = 0\).
Chọn A.