Hướng dẫn giải Tự luận Bài 13. Điện thế và thế năng điện (trang 48, 49, 50, 51, 52) – SBT Vật lí 11 Chân trời sáng tạo. Hướng dẫn: Chuyển động của electron trong điện trường đều.
Câu hỏi/Đề bài:
13.1
Đề bài:
Khi thả một electron không có vận tốc ban đầu trong một điện trường đều thì electron chuyển động như thế nào? Bỏ qua tác dụng của trọng lực.
Phương pháp giải
Chuyển động của electron trong điện trường đều
Lời giải:
Electron chuyển động nhanh dần đều ngược chiều điện trường, dọc theo phương của đường sức điện, từ điểm có điện thế thấp hơn đến điểm có điện thế cao hơn.
13.2
Đề bài:
Cho hai bản kim loại phẳng đặt song song, tích điện trái dấu. Thả một electron không vận tốc ban đầu vào điện trường giữa hai bản kim loại trên. Bỏ qua tác dụng của trọng lực. Mô tả quỹ đạo chuyển động của electron.
Phương pháp giải
Chuyển động của electron trong điện trường đều
Lời giải:
Quỹ đạo chuyển động của electron là một đường thẳng song song với các đường sức điện giữa hai bản kim loại.
13.3
Đề bài:
Cho một hạt nhân nguyên tử helium chuyển động ngược chiều đường sức điện của một điện trường đều với tốc độ ban đầu là 5.105 m/s. Sau khi chuyển động được 10 cm trong điện trường thì hạt dừng lại. Một cách gần đúng, có thể xem như hạt chỉ chịu tác dụng của lực điện. Biết rằng hạt nhân nguyên tử helium có 2 proton và khối lượng của hạt nhân này là 6,64.10-27 kg, điện tích của proton là 1,6.10-19 C. Cường độ điện trường có độ lớn bằng bao nhiêu?
Phương pháp giải
Vận dụng độ biến thiên động năng
Lời giải:
Chọn chiều dương là chiều của đường sức điện.
Độ biến thiên động năng của vật bằng công của lực điện trường:
\(\begin{array}{l}{W_d} – {W_{d0}} = A\\ \Rightarrow \frac{1}{2}{m_{He}}{v^2} – \frac{1}{2}{m_{He}}v_0^2 = {q_{He}}Ed\\ \Rightarrow E = – \frac{1}{2}\frac{{{m_{He}}v_0^2}}{{{q_{He}}d}} = – \frac{{(6,{{64.10}^{ – 27}}).{{({{5.10}^5})}^2}}}{{2.(2.1,{{6.10}^{ – 19}}).( – 0,1)}} = 25937,5\;V/m\end{array}\)
13.4
Đề bài:
Một hạt bụi mang điện tích q=1μC có khối lượng m đang nằm cân bằng trong một điện trường đều giữa hai bản kim loại phẳng nằm ngang, tích điện trái dấu và cách nhau 1,5 cm. Khi đó các đường sức điện hướng theo phương thẳng đứng. Biết hiệu điện thế giữa hai bản là 100 V, lấy g=9,8 m/s2. Xác định khối lượng của hạt bụi
Phương pháp giải
Áp dụng công thức tính lực điện
Lời giải:
Vì hạt bụi nằm cân bằng nên trọng lực cân bằng với lực điện. Ta có:
\(F = P \Rightarrow q\frac{U}{d} = mg \Rightarrow m = \frac{{qU}}{{gd}} = \frac{{{{10}^{ – 6}}.100}}{{9,8.1,{{5.10}^{ – 2}}}} \approx 0,{68.10^{ – 3\;}}kg = 0,68\;g\)
13.5
Đề bài:
Xét một vùng không gian có điện trường đều, cho 3 điểm A, B, C tạo thành một tam giác đều có độ dài các cạnh a = 6 cm, AB song song với các đường sức điện như Hình 13.3 . Biết cường độ điện trường có độ lớn E= 1000 V/m.
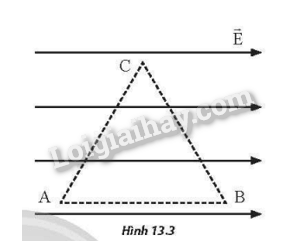
a) Tính các hiệu điện thế UAB, UBC, UCA.
b) Tính công của lực điện trường khi một proton chuyển động từ C đến B. Lấy điện tích của proton là q=1,6.10−19C
c) Nếu proton đó bắt đầu chuyển động không vận tốc ban đầu tại A thì tốc độ của proton đó khi đến B là bao nhiêu? Lấy khối lượng của proton là m=1,67.10−27 kg.
Phương pháp giải
Áp dụng công thức tính công lực điện
Lời giải:
a)
\(\begin{array}{l}{U_{AB}} = E.AB.cos0^\circ = 1000.({6.10^{ – 2}}) = 60\;V\\{U_{BC}} = E.BC.cos120^\circ = – 1000.({6.10^{ – 2}}).0,5 = – 30\;V\\{U_{CA}} = E.CA.cos120^\circ = – 1000.({6.10^{ – 2}}).0,5 = – 30\;V\end{array}\)
b) Công của lực điện trường khi một proton chuyển động từ C đến B:
\({A_{CB}} = q{U_{CB}} = (1,{6.10^{ – 19}}).30 = 4,{8.10^{ – 18}}\;J\)
c) Theo định lí động năng, ta có:
\(\begin{array}{l}{W_{dB}} – {W_{dA}} = {A_{AB}} \Rightarrow \frac{1}{2}mv_B^2 = q{U_{AB}}\\ \Rightarrow {v_B} = \sqrt {\frac{{2q{U_{AB}}}}{m}} = \sqrt {\frac{{2.(1,{{6.10}^{ – 19}}).60}}{{1,{{67.10}^{ – 27}}}}} \approx 107,{22.10^{3\;}}m/s\end{array}\)
13.6
Đề bài:
Cho 3 bản kim loại phẳng A, B, C mang điện với bản A và C tích điện âm còn bản B tích điện dương. Các bản được đặt song song nhau. Xem gần đúng điện trường giữa các bản kim loại là đều. Biết rằng khoảng cách giữa hai bản A và B là d1=3 cm còn khoảng cách giữa hai bản B và C là d2=5 cm như Hình 13.4 . Chọn gốc điện thế tại bản B. Hãy xác định điện thế tại các bản A và C nếu cường độ điện trường giữa hai bản A và B, B và C có độ lớn lần lượt là E1=200 V/m và E2=600 V/m
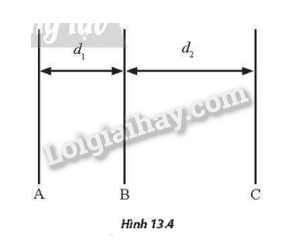
Lời giải:
Vì bản A và C tích điện âm còn bản B tích điện dương nên các vectơ cường độ điện trường \(\overrightarrow {{E_1}} \) và \(\overrightarrow {{E_2}} \) có chiều như hình bên.
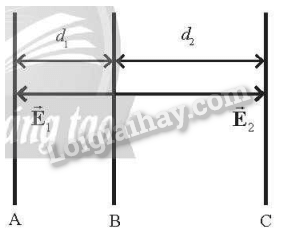
Vì gốc điện thế được chọn tại bản B nên VB=0
Điện thế tại bản A:
UBA=VB−VA=0−VA=E1d1=200.0,03=6 V⇒VA=−6 V
Điện thế tại bản C:
UBC=VB−VC=0−VC=E2d2=600.0,05=30 V⇒VC=−30 V
13.7
Đề bài:
Trong vùng không gian giữa hai tấm kim loại phẳng, tích điện trái dấu nhau và cách nhau một đoạn d = 5 cm có một hạt bụi kim loại tích điện âm, khối lượng m=2.10−6 g đang lơ lửng tại vị trí cách đều hai tấm kim loại như Hình 13.5. Biết rằng hiệu điện thế giữa hai tấm kim loại khi đó là U=1000 V. Nếu hiệu điện điện thế đột ngột giảm đến giá trị U′=850 V, hạt bụi kim loại sẽ chuyển động về tấm nào? Sau bao lâu thì hạt bụi này chạm đến một trong hai tấm kim loại nói trên? Lấy g=9,8 m/s2
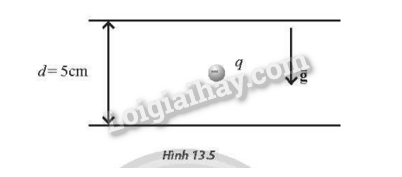
Phương pháp giải
Hạt bụi kim loại lơ lửng nên trọng lực cân bằng với lực điện
Lời giải:
Khi U=1000 V, vì hạt bụi kim loại lơ lửng nên trọng lực cân bằng với lực điện. Khi đó, bản tích điện dương sẽ ở trên và bản tích điện âm sẽ ở dưới. Ta có: \({F_d} = P \Rightarrow |q|E = mg \Rightarrow |q| = \frac{{mg}}{E} = \frac{{mgd}}{U} = \frac{{({{2.10}^{ – 9}}).9,8.({{5.10}^{ – 2}})}}{{{{2.10}^{ – 9}}}} = 1,47\;m/{s^2}\)
Thời gian hạt bụi kim loại chuyển động đến khi gặp bản âm là:
\(t = \sqrt {\frac{{2s}}{a}} = \sqrt {\frac{{2.(2,{{5.10}^{ – 2}})}}{{1,47}}} \approx 0,18s\)
13.8
Đề bài:
Ống tia âm cực (CRT) là một thiết bị thường được thấy trong dao động kí điện tử cũng như màn hình ti vi, máy tính (CRT),… Hình 13.6 cho thấy mô hình của một ống tia âm cực, bao gồm hai bản kim loại phẳng có chiều dài 8 cm, tích điện trái dấu, đặt song song và cách nhau 2 cm. Hiệu điện thế giữa hai bản kim loại là U = 12V. Một electron được phóng ra từ điểm A (cách đều hai bản kim loại) với vận tốc ban đầu có độ lớn v0=7.106 m/s và hướng dọc theo trục của ống. Cho rằng bản kim loại bên dưới có điện thế lớn hơn. Xem tác dụng của trọng lực là không đáng kể. Lấy khối lượng của electron là 9,1.10-31 kg.
a) Xác định tốc độ của electron khi vừa ra khỏi vùng không gian giữa hai bản kim loại.
b) Sau khi ra khỏi vùng không gian nói trên, hạt chuyển động thẳng đều đến đập vào màn huỳnh quang S. Biết S cách hai bản kim loại một đoạn 15 cm. Xác định vị trí trên màn S mà electron này đập vào.
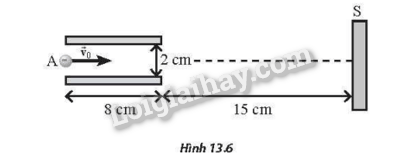
Phương pháp giải
Áp dụng công thức tính cường độ điện trường
Lời giải:
a) Cường độ điện trường giữa hai bản kim loại: \(E = \frac{U}{d} = \frac{{12}}{{{{2.10}^{ – 2}}}} = 600V/m\)
Vì lực điện hướng thẳng đứng xuống dưới nên độ lớn gia tốc trên phương thẳng đứng của electron là: \({a_y} = \frac{{\left| q \right|E}}{m} = \frac{{1,{{6.10}^{ – 19}}.600}}{{9,1 \cdot {{10}^{ – 31}}}} \approx 1,05 \cdot {10^{14}}\;m/{s^2}\)

Thời gian để electron ra khỏi vùng không gian giữa hai bản kim loại là:
\(t = \frac{l}{{{v_x}}} = \frac{{8 \cdot {{10}^{ – 2}}}}{{{{7.10}^6}}} \approx 11,43 \cdot {10^{ – 9}}\;s\)
với l=8 cm là chiều dài bản kim loại phẳng.
Thành phần vận tốc của hạt theo phương thẳng đứng khi hạt vừa ra khỏi vùng không gian giữa hai bản kim loại: \({v_y} = {a_y}t = (1,{05.10^{14}}).(11,{43.10^{ – 9}}) \approx 1,{2.10^{6\;}}m/s\)
Tốc độ của electron khi vừa ra khỏi vùng không gian giữa hai bản kim loại:\(v = \sqrt {v_x^2 + v_y^2} = \sqrt {{{({{7.10}^6})}^2} + {{(1,{{2.10}^6})}^2}} \approx 7,{1.10^{6\;}}m/s\)
b) Độ lệch của hạt so với ban đầu theo phương thẳng đứng khi hạt vừa ra khỏi vùng không gian giữa hai bản kim loại là: \(y = \frac{1}{2}{a_y}{t^2} = \frac{1}{2}(1,{05.10^{14}}){(11,{43.10^{ – 9}})^2} \approx 6,{86.10^{ – 3\;}}m\)
Vì sau đó hạt chuyển động thẳng đều nên thành phần vx, vy vẫn không thay đổi. Khi hạt đến đập vào màn huỳnh quang S, ta có:\(\left\{ \begin{array}{l}{s_x} = {v_x}t\prime \\{s_y} = {v_y}t\prime \end{array} \right. \Rightarrow {s_y} = {v_y}\frac{{{s_x}}}{{{v_x}}} = 1,{2.10^6}\frac{{0,15}}{{{{7.10}^6}}} \approx 25,{71.10^{ – 3\;}}m\)
Vị trí hạt chạm vào màn S cách trục của ống một đoạn:\(y + {s_y} = 6,{86.10^{ – 3}} + 25,{71.10^{ – 3}} = 32,{57.10^{ – 3}}\;m\)
13.9
Đề bài:
Cho quả cầu kim loại A mang điện tích qA=3μC được giữ cố định trên một giá đỡ cách điện. Một vật nhỏ B có khối lượng m = 0.5 g mang điện tích qB=8μC bay từ rất xa tiến lại gần quả cầu A như Hình 13.7. Khi tâm hai quả cầu cách nhau một đoạn d = 0,5 m thì tốc độ của quả cầu B là v = 20 m/s. Bỏ qua lực hấp dẫn giữa hai quả cầu và tác dụng của trọng lực. Xem gần đúng các quả cầu là các điện tích điểm. Biết rằng thế năng điện của quả cầu B được xác định bằng biểu thức \({W_t} = \frac{{k{q_A}{q_B}}}{r}\) với r là khoảng cách giữa hai quả cầu. Hãy xác định:
a) Khoảng cách ngắn nhất giữa hai quả cầu.
b) Tốc độ của quả cầu B khi khoảng cách giữa hai quả cầu là 0,8 m và khi chúng ở rất xa nhau.

Phương pháp giải
Áp dụng định luật bảo toàn cơ năng
Lời giải:
a) Khi khoảng cách giữa hai quả cầu đạt cực tiểu thì động năng của quả cầu B bằng 0. Áp dụng định luật bảo toàn cơ năng: \(\frac{1}{2}m{v^2} + \frac{{k{q_A}{q_B}}}{d} = 0 + \frac{{k{q_A}{q_B}}}{{{r_{\min }}}} \Rightarrow {r_{\min }} = \frac{1}{{\frac{{m{v^2}}}{{2k{q_A}{q_B}}} + \frac{1}{d}}} = \frac{1}{{\frac{{(0,{{5.10}^{ – 3}}){{.20}^2}}}{{2.({{9.10}^9}).({{3.10}^{ – 6}}).({{8.10}^{ – 6}})}} + \frac{1}{{0,5}}}} \approx 0,41\;m\)
b) Khi khoảng cách giữa hai quả cầu là r1=0,8 m, ta có:
\(\frac{1}{2}m{v^2} + \frac{{k{q_A}{q_B}}}{d} = \frac{1}{2}mv_1^2 + \frac{{k{q_A}{q_B}}}{{{r_1}}} \Rightarrow {v_1} = \sqrt {{v^2} + \frac{{2k{q_A}{q_B}}}{m}\left( {\frac{1}{d} – \frac{1}{{{r_1}}}} \right)} \Rightarrow {v_1} = \sqrt {{{20}^2} + \frac{{2.({{9.10}^9}).({{3.10}^{ – 6}}).({{8.10}^{ – 6}})}}{{0,{{5.10}^{ – 3}}}}\left( {\frac{1}{{0,5}} – \frac{1}{{0,8}}} \right)} \approx 32,37\;m/s\)Khi quả cầu B tiến ra vô cùng thì thế năng điện bằng không, ta có:
\(\frac{1}{2}m{v^2} + \frac{{k{q_A}{q_B}}}{d} = \frac{1}{2}mv_2^2 + 0 \Rightarrow {v_2} = \sqrt {{v^2} + \frac{{2k{q_A}{q_B}}}{{md}}} \Rightarrow {v_2} = \sqrt {{{20}^2} + \frac{{2.({{9.10}^9}).({{3.10}^{ – 6}}).({{8.10}^{ – 6}})}}{{0,{{5.10}^{ – 3}}.0,5}}} \approx 46,13\;m/s\)