Đáp án 3.32 – 3.43 Chủ đề 3. Điện trường – SBT Vật lí 11 Cánh diều. Gợi ý: Vận dụng kiến thức đã học về điện thế, thế năng.
Câu hỏi/Đề bài:
III. ĐIỆN THẾ, HIỆU ĐIỆN THẾ, TỤ ĐIỆN
3.32. Một electron được thả cho chuyển động trong một điện trường đều từ trạng thái nghỉ. Sau khi đi được một đoạn xác định trong điện trường thì
A. thế năng điện của điện trường tăng.
B. thế năng điện của điện trường giảm.
C. thế năng điện của điện trường giữ nguyên.
D. thế năng điện của electron tăng.
Hướng dẫn:
Vận dụng kiến thức đã học về điện thế, thế năng:
– Với mốc thế năng tại vô cùng, thế năng của điện tích q tại điểm M trong điện trường, cách bản âm một đoạn d là: \({W_M} = {A_{M\infty }} = qEd\)
– Điện thế tại một điểm trong điện trường đặc trưng cho điện trường tại điểm đó về thế năng: \({V_M} = \frac{{{A_{M\infty }}}}{q}\)
Lời giải:
Đáp án: B. thế năng điện của điện trường giảm.
3.33. Hình 3.9 là đồ thị biểu diễn điện thế theo vị trí. Nếu một hạt mang điện dương được đặt tại điểm A thì nó sẽ
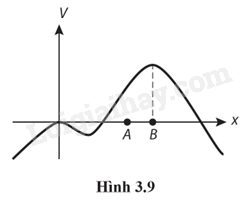
A. chuyển động sang phải.
B. chuyển động sang trái.
C. đứng yên nguyên tại điểm A.
D. dao động quanh điểm B.
Hướng dẫn:
Vận dụng kiến thức đã học về điện thế, thế năng:
– Với mốc thế năng tại vô cùng, thế năng của điện tích q tại điểm M trong điện trường, cách bản âm một đoạn d là: \({W_M} = {A_{M\infty }} = qEd\)
– Điện thế tại một điểm trong điện trường đặc trưng cho điện trường tại điểm đó về thế năng: \({V_M} = \frac{{{A_{M\infty }}}}{q}\)
Lời giải:
Đáp án: B. chuyển động sang trái.
3.34. Nếu một hạt mang điện âm được đặt tại điểm B trong Hình 3.9 và được đẩy nhẹ về phía bên phải, thì sau đó nó sẽ
A. đi sang phải và không quay lại.
B. đi sang trái và không quay lại.
C. dừng lại ở điểm B.
D. dao động quanh điểm B.
Hướng dẫn:
Vận dụng kiến thức đã học về điện thế, thế năng:
– Với mốc thế năng tại vô cùng, thế năng của điện tích q tại điểm M trong điện trường, cách bản âm một đoạn d là: \({W_M} = {A_{M\infty }} = qEd\)
– Điện thế tại một điểm trong điện trường đặc trưng cho điện trường tại điểm đó về thế năng: \({V_M} = \frac{{{A_{M\infty }}}}{q}\)
Lời giải:
Đáp án: D. dao động quanh điểm B.
3.35. Một electron ban đầu ở trạng thái nghỉ tăng tốc qua hiệu điện thế 1 V, thu được động năng Wđe , trong khi một proton, ban đầu cũng ở trạng thái nghỉ, tăng tốc qua hiệu điện thế -1 V, thu được động năng Wđp . Phát biểu nào sau đây đúng?
A. Động năng của electron bằng động năng của proton, Wđe = Wđp.
B. Động năng của electron nhỏ hơn động năng của proton, Wđe < Wđp.
C. Động năng của electron lớn hơn động năng của proton, Wđe > Wđp.
D. Không thể xác định được câu trả lời từ thông tin đã cho.
Hướng dẫn:
Vận dụng kiến thức về thế năng và năng lượng:
– Với mốc thế năng tại vô cùng, thế năng của điện tích q tại điểm M trong điện trường, cách bản âm một đoạn d là: \({W_M} = {A_{M\infty }} = qEd\)
– Điện thế tại một điểm trong điện trường đặc trưng cho điện trường tại điểm đó về thế năng: \({V_M} = \frac{{{A_{M\infty }}}}{q}\)
– Định luật bảo toàn năng lượng: Wt + Wđ = const
Lời giải:
Thế năng của electron: Wte = Vq = 1.(-e) = -e
Thế năng của proton: Wtp = Vq = (-1).e = -e
Wte = Wtp
=> Wđe = Wđp
Đáp án: A. Động năng của electron bằng động năng của proton, Wđe = Wđp.
3.36. Một tụ điện gồm hai bản mỏng song song với nhau, một bản có diện tích bằng hai lần bản kia. Nối hai bản tụ với hai cực của một bộ pin. Phát biểu nào sau đây là đúng?
A. Bản lớn có điện tích lớn hơn bản nhỏ.
B. Bản lớn có ít điện tích hơn bản nhỏ.
C. Các bản có điện tích bằng nhau nhưng ngược dấu.
D. Bản lớn có điện tích bằng hai lần bản nhỏ.
Hướng dẫn:
Vận dụng kiến thức đã học về tụ điện:
– Tụ điện là dụng cụ chứa điện tích.
– Tụ phẳng gồm hai bản mỏng song song và ở giữa có một lớp điện môi.
– Khi được tích điện, hai bản có điện tích bằng nhau nhưng ngược dấu.
Lời giải:
Đáp án: C. Các bản có điện tích bằng nhau nhưng ngược dấu.
3.37. Một proton được thả cho chuyển động từ trạng thái nghỉ, ở vị trí x = – 2,00 cm trong một điện trường đều có cường độ điện trường với độ lớn 1,50.103 N/C và hướng theo chiều x dương.
a) Tìm độ biến thiên thế năng điện trường và tốc độ của proton khi nó đi đến vị trí x = 5,00 cm.
b) Một electron được bắn theo theo chiều x dương từ cùng một vị trí thả proton. Tìm độ biến thiên thế năng điện trường và tốc độ ban đầu của electron khi electron đi đến vị trí x = 12,0 cm. Biết rằng khi đến vị trí đó, tốc độ của electron đã giảm một nửa.
c) Nếu đổi chiều của điện trường và electron được thả cho chuyển động (không vận tốc ban đầu) ở x = 3,00 cm thì thế năng điện trường đã thay đổi bao nhiêu khi electron đi đến vị trí x = 7,00 cm?
Hướng dẫn:
Vận dụng kiến thức đã học về thế năng và tốc độ của vật chuyển động biến đổi đều:
– Độ biến thiên thế năng điện trường: \(\Delta {{\rm{W}}_t} = qE\Delta d\)
– Độ biến thiên vận tốc trong chuyển động thẳng biến đổi đều: \(\left| {v_2^2 – v_1^2} \right| = 2{\rm{as}}\)
– Định luật II Newton: \(\sum {\vec F} = m\vec a \Rightarrow \vec a = \frac{{\sum {\vec F} }}{m}\)
Lời giải:
a) Gia tốc của điện tích là:
\(a = \frac{F}{m} = \frac{{qE}}{m} = \frac{{1,{{6.10}^{ – 19}}.1,{{5.10}^3}}}{{1,{{67.10}^{ – 27}}}} = 1,{44.10^{11}}{\rm{ m/}}{{\rm{s}}^{\rm{2}}}\)
Tốc độ của proton khi đến vị trí x = 5,00 cm:
\(\begin{array}{l}\left| {v_2^2 – v_1^2} \right| = 2{\rm{as}}\\ \Leftrightarrow {v_2} = \sqrt {2{\rm{as}} + v_1^2} = \sqrt {2.1,{{44.10}^{11}}.\left( {5 – \left( { – 2} \right)} \right){{.10}^{ – 2}}} \\ \Leftrightarrow {v_2} = 1,{42.10^6}{\rm{ m/s}}\end{array}\)
Độ biến thiên thế năng điện trường:
\(\Delta {{\rm{W}}_t} = – 1,{6.10^{ – 19}}.1,{50.10^3}.\left( {5 – \left( { – 2} \right)} \right){.10^{ – 2}} = – 1,{68.10^{ – 17}}{\rm{ J}}\)
b) Độ biến thiên thế năng điện trường:
\(\Delta {{\rm{W}}_t} = – \left( { – 1,{{6.10}^{ – 19}}} \right).1,{50.10^3}.\left( {12 – \left( { – 2} \right)} \right){.10^{ – 2}} = 3,{36.10^{ – 17}}{\rm{ J}}\)
\(\begin{array}{l}\left| {v_2^2 – v_1^2} \right| = 2{\rm{as}}\\\left| {v_2^2 – 2v_2^2} \right| = 2{\rm{as}}\\ \Rightarrow {v_2} = \sqrt {2{\rm{as}}} = \sqrt {2.1,{{44.10}^{11}}.\left( {12 – \left( { – 2} \right)} \right){{.10}^{ – 2}}} \\ \Leftrightarrow {v_2} = 0,{2.10^6}{\rm{ m/s}}\\ \Rightarrow {v_1} = 0,{4.10^6}{\rm{ m/s}}\end{array}\)
c) Độ biến thiên thế năng điện trường:
\(\Delta {{\rm{W}}_t} = – \left( { – 1,{{6.10}^{ – 19}}} \right).\left( { – 1,{{50.10}^3}} \right).\left( {7 – 3} \right){.10^{ – 2}} = – 9,{6.10^{ – 18}}{\rm{ J}}\)
3.38. Một máy kích thích tim được sạc đầy chứa 1,20 kJ năng lượng trong tụ điện của máy. Biết điện dung của tụ điện là 1,10.10-4 F.
a) Tìm hiệu điện thế cần thiết giữa hai bản tụ điện để lưu trữ 1,20 kJ. b) Khi máy phóng điện qua một bệnh nhân, năng lượng điện 6,00.102 J được truyền đi trong 2,50 ms. Tính công suất trung bình được cung cấp cho bệnh nhân.
Hướng dẫn:
Vận dụng kiến thức đã học về:
– Hiệu điện thế giữa hai bản tụ điện: \(U = \sqrt {\frac{{2{\rm{W}}}}{C}} \)
– Công suất trung bình: \(P = \frac{A}{t}\)
Lời giải:
a) Hiệu điện thế giữa hai bản tụ điện:
\(U = \sqrt {\frac{{2{\rm{W}}}}{C}} = \sqrt {\frac{{2.1,{{2.10}^3}}}{{1,{{1.10}^{ – 4}}}}} = 4,{67.10^3}{\rm{ V}}\)
b) Công suất trung bình cung cấp cho bệnh nhân:
\(P = \frac{A}{t} = \frac{{600}}{{2,{{5.10}^{ – 3}}}} = 2,{4.10^5}{\rm{ W}}\)
3.39. Trong các máy gia tốc hạt (cyclotron), các hạt tích điện được gia tốc giống như cách chúng được gia tốc trong các ống phóng điện tử, tức là thông qua một hiệu điện thế. Giả sử một proton được bơm với tốc độ ban đầu 1,00.106 m/s vào giữa hai bản phẳng cách nhau 5,00 cm (Hình 3.10). Sau đó, proton tăng tốc và thoát ra ngoài qua lỗ ở bản đối diện. Coi điện trường giữa hai bản là đều. Hướng x dương là hướng sang phải. a) Tìm hiệu điện thế giữa hai bản, nếu tốc độ thoát của proton là 3,00.106 m/s. b) Tính độ lớn cường độ điện trường giữa hai bản
Hướng dẫn:
Vận dụng kiến thức đã học về:
– Định luật bảo toàn cơ năng: \({W_{\rm{d}}} + {W_t} = const\)
– Với mốc thế năng tại vô cùng, thế năng của điện tích q tại điểm M trong điện trường, cách bản âm một đoạn d là: \({W_M} = {A_{M\infty }} = qEd = qU\)
– Liên hệ giữa giá trị cường độ điện trường đều và hiệu điện thế: U = Ed
Lời giải:
a) Theo định luật bảo toàn cơ năng, ta có:
\(\begin{array}{l}\Delta {{\rm{W}}_d} + \Delta {{\rm{W}}_t} = \Delta {{\rm{W}}_d} + qU = 0\\ \Rightarrow U = – \frac{{\Delta {{\rm{W}}_d}}}{q} = – \frac{{{m_p}}}{{2q}}\left( {v_2^2 – v_1^2} \right)\\ \Rightarrow U = – \frac{{1,{{67.10}^{ – 27}}}}{{2.1,{{6.10}^{ – 19}}}}\left( {{{\left( {{{3.10}^6}} \right)}^2} – {{\left( {{{10}^6}} \right)}^2}} \right)\\ \Leftrightarrow U = – 4,{18.10^4}{\rm{ V}}\end{array}\)
b) Cường độ điện trường giữa hai bản:
\(E = \frac{U}{d} = \frac{{4,{{18.10}^4}}}{{0,05}} = 8,{36.10^5}{\rm{ N/C}}\)
3.40. Một tụ điện gồm hai bản song song, khoảng cách giữa hai bản là d = 1,00.10-3 m. Điện dung của tụ điện là C = 1,77 pF và hiệu điện thế giữa hai bản của tụ điện là 3,00 V.
a) Tính độ lớn điện tích của tụ điện. b) Tính độ lớn của cường độ điện trường giữa các bản.
Hướng dẫn:
Vận dụng kiến thức đã học về tụ điện:
– Điện tích của tụ điện: Q = CU
– Liên hệ giữa giá trị cường độ điện trường đều và hiệu điện thế: U = Ed
Lời giải:
a) Điện tích của tụ điện:
\(Q = CU = 1,{77.10^{ – 12}}.3 = 5,{31.10^{ – 12}}{\rm{ C}}\)
b) Cường độ điện trường giữa các bản:
\(E = \frac{U}{d} = \frac{3}{{{{10}^{ – 3}}}} = 3000{\rm{ V/m}}\)
3.41. Bộ tụ điện ghép song song (Hình 3.11) gồm: C1 = 3,00 μF; C2 = 6,00 μF; C3 = 12,0 μF; C4 = 24,0 μF. Hiệu điện thế U = 18,0 V.
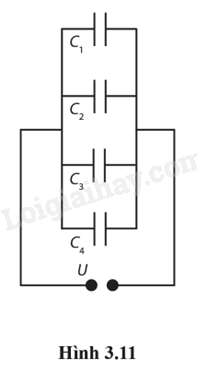a) Xác định điện dung của tương đương của bộ tụ điện. b) Tìm điện tích trên tụ điện có điện dung C3. c) Tìm tổng điện tích của bộ tụ điện.
Hướng dẫn:
Vận dụng kiến thức đã học về tụ điện ghép song song:
– Điện dung: \(C = {C_1} + {C_2} + … + {C_n}\)
– Hiệu điện thế: \(U = {U_1} = {U_2} = … = {U_n}\)
– Điện tích: \(Q = {Q_1} + {Q_2} + … + {Q_n}\)
– Liên hệ giữa điện tích, điện dung và hiệu điện thế của tụ điện: \(Q = CU\)
Lời giải:
a) \(C = {C_1} + {C_2} + {C_3} + {C_4} = 3 + 6 + 12 + 24 = 45{\rm{ }}\mu {\rm{F}}\)
b) \({Q_3} = {C_3}.{U_3} = {C_3}.U = 12.18 = 216{\rm{ }}\mu {\rm{C}}\)
c) \(Q = CU = 45.{\rm{18 = 810 }}\mu {\rm{C}}\)
3.42. Bốn tụ điện được mắc nối tiếp (Hình 3.12). C1 = 3,0 μF; C2 = 6,0 μF; C3 = 12 μF; C4 = 24 μF; U = 18 V.
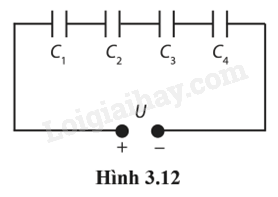a) Tính điện dung tương đương của bộ tụ điện. b) Tính điện tích của tụ điện có điện dung C3. c) Tìm hiệu điện thế giữa hai bản của tụ điện có điện dung C3.
Hướng dẫn:
Vận dụng kiến thức đã học về tụ điện ghép nối tiếp:
– Điện dung: \(\frac{1}{C} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} + … + \frac{1}{{{C_n}}}\)
– Hiệu điện thế: \(U = {U_1} + {U_2} + … + {U_n}\)
– Điện tích: \(Q = {Q_1} = {Q_2} = … = {Q_n}\)
– Liên hệ giữa điện tích, điện dung và hiệu điện thế của tụ điện: \(Q = CU\)
Lời giải:
a) \(\begin{array}{l}\frac{1}{C} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} + \frac{1}{{{C_3}}} + \frac{1}{{{C_4}}} = \frac{1}{3} + \frac{1}{6} + \frac{1}{{12}} + \frac{1}{{24}} = 0,625\\ \Rightarrow C = 1,6{\rm{ }}\mu {\rm{F}}\end{array}\)
b) \({Q_3} = Q = C.U = 1,6.18 = 29{\rm{ }}\mu {\rm{C}}\)
c) \({U_3} = \frac{{{Q_3}}}{{{C_3}}} = \frac{{29}}{{12}} = 2,4{\rm{ V}}\)
3.43. Bộ tụ điện ghép như Hình 3.13. Điện dung của các tụ điện có giá trị: C1 = 4,0 μF; C2 = 1,0 μF; C3 = 3,0 μF; C4 = 84,0 μF; C5 = 6,0 μF; C6 = 2,0 μF; a) Tính điện dung tương đương của bộ tụ điện. b) Hiệu điện thế giữa A và B là 12 V. Tìm điện tích của tụ điện C1 và hiệu điện thế giữa hai bản tụ.
Hướng dẫn:
Vận dụng kiến thức đã học về tụ điện:
Liên hệ giữa điện tích, điện dung và hiệu điện thế của tụ điện: \(Q = CU\)
Tụ điện ghép song song:
– Điện dung: \(C = {C_1} + {C_2} + … + {C_n}\)
– Hiệu điện thế: \(U = {U_1} = {U_2} = … = {U_n}\)
– Điện tích: \(Q = {Q_1} + {Q_2} + … + {Q_n}\)
Tụ điện ghép nối tiếp:
– Điện dung: \(\frac{1}{C} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} + … + \frac{1}{{{C_n}}}\)
– Hiệu điện thế: \(U = {U_1} + {U_2} + … + {U_n}\)
– Điện tích: \(Q = {Q_1} = {Q_2} = … = {Q_n}\)
Lời giải:
a)
\(\begin{array}{l}{C_{23}} = {C_2} + {C_3} = 1 + 3 = 4{\rm{ }}\mu {\rm{F}}\\\frac{1}{{{C_{123}}}} = \frac{1}{{{C_1}}} + \frac{1}{{{C_{23}}}} = \frac{1}{4} + \frac{1}{4} = \frac{1}{2} \Rightarrow {C_{123}} = 2{\rm{ }}\mu {\rm{F}}\\{C_{56}} = {C_5} + {C_6} = 6 + 2 = 8{\rm{ }}\mu {\rm{F}}\\\frac{1}{{{C_{456}}}} = \frac{1}{{{C_4}}} + \frac{1}{{{C_{56}}}} = \frac{1}{{84}} + \frac{1}{8} = \frac{{23}}{{168}} \Rightarrow {C_{456}} = 7,3{\rm{ }}\mu {\rm{F}}\\C = {C_{123}} + {C_{456}} = 2 + 7,3 = 9,3{\rm{ }}\mu {\rm{F}}\end{array}\)
b)
\(\begin{array}{l}{U_{123}} = {U_{456}} = U = 12{\rm{ V}}\\{Q_1} = {Q_{123}} = {C_{123}}{U_{123}} = 2.12 = 24{\rm{ }}\mu {\rm{C}}\\{U_1} = \frac{{{Q_1}}}{{{C_1}}} = \frac{{24}}{4} = 6{\rm{ V}}\end{array}\)