Lời giải 3.27 – 3.31 Chủ đề 3. Điện trường – SBT Vật lí 11 Cánh diều. Hướng dẫn: Vận dụng kiến thức đã học về điện trường.
Câu hỏi/Đề bài:
3.27. Cường độ điện trường tại điểm cách một điện tích điểm 0,20 m có độ lớn 2,8.106 N/C, hướng về phía điện tích. Tìm độ lớn và dấu của điện tích.
Hướng dẫn:
Vận dụng kiến thức đã học về điện trường:
– Cường độ điện trường tại một điểm là đại lượng vecto có phương và chiều là phương chiều của lực điện tác dụng lên điện tích: \(\vec E = \frac{{\vec F}}{q}\)
– Với điện tích điểm có giá trị Q, đặt trong chân không, độ lớn của cường độ điện trường là: \(E = \frac{F}{q} = k\frac{{\left| Q \right|}}{{{r^2}}}\)
Lời giải:
Điện trường hướng về phía điện tích nên đây là điện tích âm.
Điện tích có độ lớn là:
\(\left| q \right| = \frac{{E{r^2}}}{k} = \frac{{2,{{8.10}^6}.0,{2^2}}}{{{{9.10}^9}}} = 1,{2.10^{ – 5}}{\rm{ C}}\)
3.28. Hai điện tích điểm -40,0 μC và 50,0 μC đặt cách nhau 12,0 cm. Tìm cường độ điện trường tại điểm ở chính giữa đoạn thẳng nối hai điện tích này.
Hướng dẫn:
Vận dụng kiến thức đã học về điện trường:
– Cường độ điện trường tại một điểm là đại lượng vecto có phương và chiều là phương chiều của lực điện tác dụng lên điện tích: \(\vec E = \frac{{\vec F}}{q}\)
– Với điện tích điểm có giá trị Q, đặt trong chân không, độ lớn của cường độ điện trường là: \(E = \frac{F}{q} = k\frac{{\left| Q \right|}}{{{r^2}}}\)
Lời giải:
Cường độ điện trường tại điểm chính giữa đoạn thẳng nối hai điện tích do hai điện tích này gây ra lần lượt là E1, E2.
\(\begin{array}{l}{E_1} = k\frac{{\left| {{q_1}} \right|}}{{{r^2}}} = {9.10^9}\frac{{\left| { – {{40.10}^{ – 6}}} \right|}}{{0,{{06}^2}}} = {10^8}{\rm{ N/C}}\\{E_2} = k\frac{{\left| {{q_2}} \right|}}{{{r^2}}} = {9.10^9}\frac{{\left| {{{50.10}^{ – 6}}} \right|}}{{0,{{06}^2}}} = 1,{25.10^8}{\rm{ N/C}}\end{array}\)
Điện trường tại điểm ở chính giữa đoạn thẳng nối hai điện tích này là E
\(\vec E = {\vec E_1} + {\vec E_2}\)
Mà \({\vec E_1} \uparrow \uparrow {\vec E_2}\)
Nên E = E1 + E2 và \(\vec E \uparrow \uparrow {\vec E_1} \uparrow \uparrow {\vec E_2}\)
\(E = {E_1} + {E_2} = {10^8}{\rm{ + }}1,{25.10^8} = 2,{25.10^8}{\rm{ N/C}}\)
3.29. Hai điểm A và B cách nhau 5,0 cm. Điện tích tại A là 46 μC, tại B là 82 μC. Tìm cường độ điện trường tại điểm C cách B một đoạn 4,0 cm biết AB vuông góc với BC. (Hình 3.7).
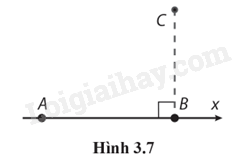
Hướng dẫn:
Vận dụng kiến thức đã học về điện trường và lượng giác:
– Cường độ điện trường tại một điểm là đại lượng vecto có phương và chiều là phương chiều của lực điện tác dụng lên điện tích: \(\vec E = \frac{{\vec F}}{q}\)
– Với điện tích điểm có giá trị Q, đặt trong chân không, độ lớn của cường độ điện trường là: \(E = \frac{F}{q} = k\frac{{\left| Q \right|}}{{{r^2}}}\)
– Định lí cosin: \({a^2} = {b^2} + {c^2} – 2bc\cos A\)
Lời giải:

\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{5^2} + {4^2}} = \sqrt {41} = 6,4{\rm{ cm}}\)
Điện trường tại điểm C: \({\vec E_C} = {\vec E_{AC}} + {\vec E_{BC}}\)
\({E_{AC}} = k\frac{{\left| {{q_A}} \right|}}{{A{C^2}}} = {9.10^9}.\frac{{\left| {{{46.10}^{ – 6}}} \right|}}{{{{41.10}^{ – 2.2}}}} = {10^8}{\rm{ N/C}}\)
\({E_{BC}} = k\frac{{\left| {{q_B}} \right|}}{{B{C^2}}} = {9.10^9}.\frac{{\left| {{{82.10}^{ – 6}}} \right|}}{{0,{{04}^2}}} = 4,{6.10^8}{\rm{ N/C}}\)
\(\begin{array}{l}\cos A\hat CB = \frac{{BC}}{{AC}} = \frac{4}{{6,4}} = 0,625\\ \Rightarrow A\hat CB = 51,{3^ \circ }\end{array}\)
\(\begin{array}{l} \Rightarrow E_C^2 = E_{AC}^2 + E_{BC}^2 – 2{F_{AC}}{F_{BC}}\cos \left( {180 – 51,3} \right)\\E_C^2 = {\left( {{{10}^8}} \right)^2} + {\left( {4,{{6.10}^8}} \right)^2} – {2.10^8}.4,{6.10^8}.\cos 128,7\\E_C^2 = 2,{8.10^{17}}\\ \Rightarrow {E_C} = 5,{3.10^8}{\rm{ N}}\end{array}\)
3.30. Hai điện tích được đặt tại hai điểm A và B (Hình 3.8). Điện tích tại A là 14 nC, tại B là 12 nC. AN = NB = 6,0 cm; MN = 8,0 cm. MN vuông góc với AB. Tìm cường độ điện trường tại điểm M.
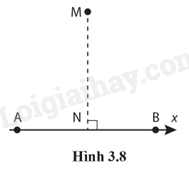
Hướng dẫn:
Vận dụng kiến thức đã học về điện trường và lượng giác:
– Cường độ điện trường tại một điểm là đại lượng vecto có phương và chiều là phương chiều của lực điện tác dụng lên điện tích: \(\vec E = \frac{{\vec F}}{q}\)
– Với điện tích điểm có giá trị Q, đặt trong chân không, độ lớn của cường độ điện trường là: \(E = \frac{F}{q} = k\frac{{\left| Q \right|}}{{{r^2}}}\)
– Định lí cosin: \({a^2} = {b^2} + {c^2} – 2bc\cos A\)
Lời giải:

\(\Delta MAN\) vuông tại N.
\(\begin{array}{l}AM = \sqrt {A{N^2} + M{N^2}} = \sqrt {{6^2} + {8^2}} = 10{\rm{ cm}}\\\sin AMN = \frac{{NA}}{{MA}} = \frac{6}{{10}} = 0,6\\ \Rightarrow A\hat MN = 36,{87^ \circ }\end{array}\)
Xét \(\Delta MAB\)
MN là đường trung trực của AB.
\( \Rightarrow \Delta MAB\) cân tại M
\(A\hat MB = N\hat MA + N\hat MB = 2.N\hat MA = 73,{74^ \circ }\)
Điện trường tại điểm M: \({\vec E_M} = {\vec E_{AM}} + {\vec E_{BM}}\)
\({E_{AM}} = k\frac{{\left| {{q_A}} \right|}}{{A{M^2}}} = {9.10^9}.\frac{{\left| {{{14.10}^{ – 9}}} \right|}}{{0,{1^2}}} = 12,{6.10^3}{\rm{ N/C}}\)
\({E_{BM}} = k\frac{{\left| {{q_B}} \right|}}{{B{M^2}}} = {9.10^9}.\frac{{\left| {{{12.10}^{ – 9}}} \right|}}{{0,{1^2}}} = 10,{8.10^3}{\rm{ N/C}}\)
\(\begin{array}{l} \Rightarrow E_M^2 = E_{AM}^2 + E_{BM}^2 – 2{E_{AM}}{E_{BM}}\cos \left( {180 – 73,74} \right)\\E_1^2 = {\left( {12,{{6.10}^3}} \right)^2} + {\left( {10,{{8.10}^3}} \right)^2} – 2.12,{6.10^3}.10,{8.10^3}.\cos 106,26\\E_M^2 = 351,{6.10^6}\\ \Rightarrow {E_M} = 18,{8.10^3}{\rm{ N}}\end{array}\)
Áp dụng định lí cosin:
\(\begin{array}{l}\cos {M_2} = \frac{{E_{AM}^2 + E_M^2 – E_{BM}^2}}{{2.{E_{AM}}{E_{BM}}}} = \frac{{{{\left( {12,{{6.10}^3}} \right)}^2} + {{\left( {18,{{8.10}^3}} \right)}^2} – {{\left( {10,{{8.10}^3}} \right)}^2}}}{{2.12,{{6.10}^3}.18,{{8.10}^3}}}\\ \Rightarrow {{\hat M}_2} = 33,{4^ \circ }\\{{\hat M}_1} = M\hat AN = {90^ \circ } – N\hat MA = {90^ \circ } – 36,{87^ \circ } = 53,{13^ \circ }\\{E_M}\hat Mx = {{\hat M}_1} + {{\hat M}_2} = 53,{13^ \circ } + 33,{4^ \circ } = {87^ \circ }\end{array}\)
3.31. Người ta làm thí nghiệm, cho những giọt dầu nhỏ mang điện tích âm với độ lớn điện tích khác nhau rơi trong điện trường (đặt trong chân không). Biết cường độ điện trường có độ lớn 5,92.104 N/C và có hướng thẳng đứng xuống dưới.
a) Xét một giọt dầu lơ lửng trong vùng có điện trường (lực điện tác dụng lên giọt dầu cân bằng với lực hấp dẫn của Trái Đất tác dụng lên nó). Biết khối lượng của giọt dầu là 2,93.10-15 kg, tìm điện tích của giọt dầu. b) Một giọt dầu khác có cùng khối lượng nhưng rơi với tốc độ ban đầu bằng không và trong 0,250 s rơi được 10,3 cm. Tìm điện tích của giọt dầu này. Lấy g = 9,80 m/s2.
Hướng dẫn:
Vận dụng kiến thức đã học về điện trường và chuyển động ném xiên:
– Cường độ điện trường tại một điểm là đại lượng vecto có phương và chiều là phương chiều của lực điện tác dụng lên điện tích: \(\vec E = \frac{{\vec F}}{q}\)
– Với điện tích điểm có giá trị Q, đặt trong chân không, độ lớn của cường độ điện trường là: \(E = \frac{F}{q} = k\frac{{\left| Q \right|}}{{{r^2}}}\)
– Định luật II Newton: \(\sum {\vec F} = m\vec a\)
– Phương trình ném xiên với \(\alpha = 0:{\rm{ }}y = {v_0}t + \frac{1}{2}a{t^2}\)
Lời giải:
a) Các lực tác dụng lên giọt dầu: \(\vec P;{\rm{ }}\vec F\)
Theo định luật II Newton:
\(\vec P + \vec F = m\vec a\)
Giọt dầu lơ lửng nên gia tốc của giọt dầu a = 0
\(\begin{array}{l}F = P\\ \Leftrightarrow qE = mg\\ \Rightarrow q = – \frac{{mg}}{E} = – \frac{{2,{{93.10}^{ – 15}}.9,8}}{{5,{{92.10}^4}}} = – 4,{85.10^{ – 19}}{\rm{ C}}\end{array}\)
b) Chọn chiều dương trùng với chiều chuyển động, gốc thời gian là khi bắt đầu thả rơi giọt dầu.
Giọt dầu rơi tự do với phương trình:
\(\begin{array}{l}y = {v_0}t + \frac{1}{2}a{t^2}\\ \Leftrightarrow 10,3 = \frac{1}{2}a.0,{25^2}\\ \Leftrightarrow a = 330{\rm{ cm/}}{{\rm{s}}^2} = 3,3{\rm{ m/}}{{\rm{s}}^2}\end{array}\)
Các lực tác dụng lên giọt dầu: \(\vec P;{\rm{ }}\vec F\)
Theo định luật II Newton:
\(\begin{array}{l}\vec P + \vec F = m\vec a\\ \Leftrightarrow P + F = ma\\ \Leftrightarrow mg + qE = ma\\ \Leftrightarrow q = \frac{{m\left( {a – g} \right)}}{E} = \frac{{2,{{93.10}^{–15}}\left( {3,3 – 9,8} \right)}}{{5,{{92.10}^4}}}\\ \Leftrightarrow q = 3,{22.10^{–19}}{\rm{ C}}\end{array}\)