Trả lời Luyện tập 4 Bài 23. Đường thẳng vuông góc với mặt phẳng (trang 34, 35, 36) – SGK Toán 11 Kết nối tri thức. Hướng dẫn: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó.
Câu hỏi/Đề bài:
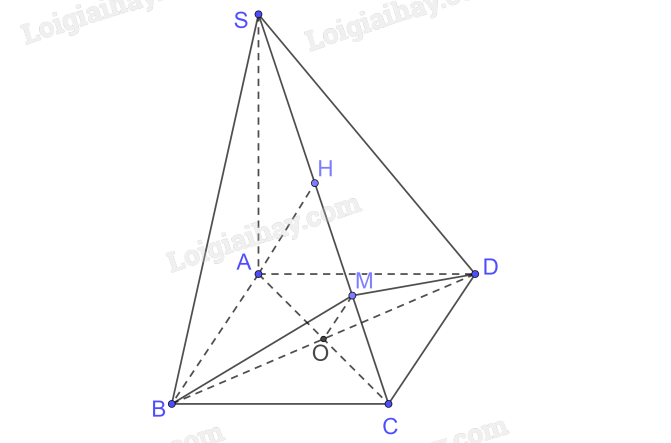
Cho hình chóp S.ABCD có đáy ABCD là một hình vuông, SA \( \bot \) (ABCD). Kẻ AH vuông góc với SC (H thuộc SC), BM vuông góc với SC (M thuộc SC). Chứng minh rằng SC \( \bot \) (MBD) và AH // (MBD).
Hướng dẫn:
– Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
– Trong 1 mặt phẳng có 2 đường thẳng cùng vuông góc với đường thẳng thứ 3 thì chúng song song.
– Đường thẳng song song với mặt phẳng nếu nó song song với 1 đường thẳng nằm trong mặt phẳng đó.
Lời giải:
\(\begin{array}{l}\left. \begin{array}{l} + )AC \bot BD\,\,\left( {hv\,\,ABCD} \right)\\SA \bot BD\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\\AC \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right)\\\left. \begin{array}{l} + )BD \bot SC\left( {BD \bot \left( {SAC} \right)} \right)\\BM \bot SC\\BD \cap BM = \left\{ B \right\}\end{array} \right\} \Rightarrow SC \bot \left( {MBD} \right)\end{array}\)
Gọi \(AC \cap BD = \left\{ O \right\}\)
\(\left. \begin{array}{l}SC \bot \left( {MBD} \right)\\OM \subset \left( {MBD} \right)\end{array} \right\} \Rightarrow SC \bot OM\)
Mà \(AH \bot SC\)
\( \Rightarrow AH//OM,OM \subset \left( {MBD} \right) \Rightarrow AH//\left( {MBD} \right)\)