Bài 7.7 trang 36 Toán 11 tập 2 – Kết nối tri thức: Cho hình chóp S. ABCD có đáy là hình chữ nhật và SA ⊥ (ABCD). Gọi M, N tương ứng là hình chiếu của A trên SB, SD

Đề bài/câu hỏi:

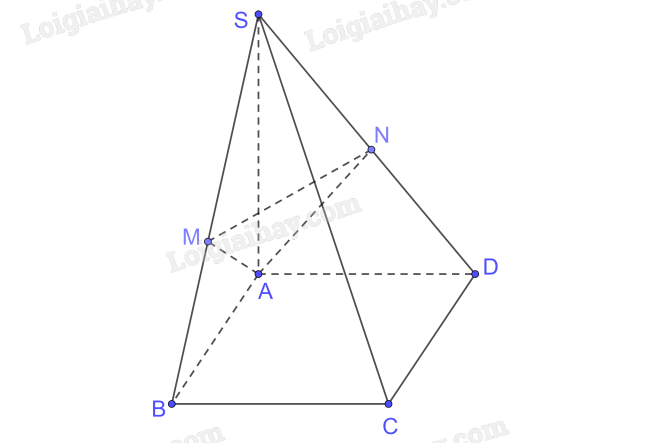
Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA \( \bot \) (ABCD). Gọi M, N tương ứng là hình chiếu của A trên SB, SD. Chứng minh rằng:

AM \( \bot \) (SBC), AN \( \bot \) (SCD), SC \( \bot \) (AMN).

Hướng dẫn:

– Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.

– Định nghĩa đường thẳng vuông góc mặt phẳng.

Lời giải:

\(\begin{array}{l}\left. \begin{array}{l} + )BC \bot AB\left( {hcn\,\,ABCD} \right)\\BC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\\AB \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right);AM \subset \left( {SAB} \right) \Rightarrow BC \bot AM\\\left. \begin{array}{l} + )CD \bot AD\left( {hcn\,\,ABCD} \right)\\CD \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\\AD \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow CD \bot \left( {SAD} \right);AN \subset \left( {SAD} \right) \Rightarrow CD \bot AN\end{array}\)

\(\begin{array}{l}\left. \begin{array}{l} + )AM \bot SB\\AM \bot BC\\SB \cap BC = \left\{ B \right\}\end{array} \right\} \Rightarrow AM \bot \left( {SBC} \right);SC \subset \left( {SBC} \right) \Rightarrow SC \bot AM\\\left. \begin{array}{l} + )AN \bot SD\\AN \bot CD\\SD \cap CD = \left\{ D \right\}\end{array} \right\} \Rightarrow AN \bot \left( {SCD} \right);SC \subset \left( {SCD} \right) \Rightarrow SC \bot AN\\\left. \begin{array}{l} + )AM \bot SC\\AN \bot SC\\AM \cap AN = \left\{ A \right\}\end{array} \right\} \Rightarrow SC \bot \left( {AMN} \right)\end{array}\)