Đáp án Luyện tập 1 Bài 30. Công thức nhân xác suất cho hai biến cố độc lập (trang 76, 77) – SGK Toán 11 Kết nối tri thức. Tham khảo: Nếu hai biến cố A và B độc lập với nhau thì P(AB) = P(A). P(B).
Câu hỏi/Đề bài:
Các học sinh lớp 11D làm thí nghiệm gieo hai loại hạt giống A và B. Xác suất để hai loại hạt giống A và B nảy mầm tương ứng là 0,92 và 0,88. Giả sử việc nảy mầm của hạt A và hạt B là độc lập với nhau. Dùng sơ đồ hình cây, tính xác suất để:
a) Hạt giống A nảy mầm còn hạt giống B không nảy mầm;
b) Hạt giống A không nảy mầm còn hạt giống B nảy mầm;
c) Ít nhất có một trong hai loại hạt giống nảy mầm.
Hướng dẫn:
Nếu hai biến cố A và B độc lập với nhau thì P(AB) = P(A).P(B).
Lời giải:
Ta dùng sơ đồ hình cây để mô tả như sau:
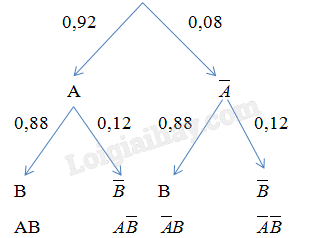
Theo sơ đồ hình cây, ta có:
a) \(P\left( {A\overline B } \right) = 0,92.0,12 = 0,1104\)
b) \(P\left( {\overline A B} \right) = 0,08.0,88 = 0,0704\)
c) \(P\left( {\overline A \overline B } \right) = 0,08.0,12 = 0,0096\)
\(P\left( {A \cup B} \right) = 1 – P\left( {\overline A \overline B } \right) = 1 – 0,0096 = 0,9904\)