Trả lời Luyện tập 1 Bài 22. Hai đường thẳng vuông góc (trang 29, 30) – SGK Toán 11 Kết nối tri thức. Tham khảo: Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song.
Câu hỏi/Đề bài:
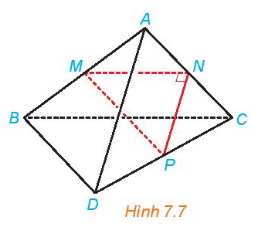
Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP). Lần lượt lấy các điểm B, C, D sao cho M, N, P tương ứng là trung điểm của AB, AC, CD (H.7.7). Chứng minh rằng AD và BC vuông góc với nhau và chéo nhau.
Hướng dẫn:
Nếu đường thẳng a vuông góc với đường thẳng b thì a có vuông góc với các đường thẳng song song với b.
Lời giải:
+) Xét tam giác ABC có
M, N lần lượt là trung điểm của AB, AC
\( \Rightarrow \) MN là đường trung bình của tam giác ABC
\( \Rightarrow \) MN // BC
Mà NP \( \bot \) MN nên NP \( \bot \) BC
Xét tam giác ADC có
N, P lần lượt là trung điểm của AC, CD
\( \Rightarrow \) PN là đường trung bình của tam giác ADC
\( \Rightarrow \) PN // AD
Mà NP \( \bot \) BC nên AD \( \bot \) BC
+) BC // MN mà \(MN \subset \left( {MNP} \right) \Rightarrow BC//\left( {MNP} \right)\)
PN // AD mà \(PN \subset \left( {MNP} \right) \Rightarrow AD//\left( {MNP} \right)\)
Vậy AD và BC chéo nhau.