Trả lời Hoạt động 7 Bài 3. Hàm số lượng giác (trang 29, 30) – SGK Toán 11 Kết nối tri thức. Tham khảo: Sử dụng định nghĩa hàm số chẵn lẻ.
Câu hỏi/Đề bài:
Cho hàm số \(y = \cot x\)
a) Xét tính chẵn, lẻ của hàm số
b) Hoàn thành bảng giá trị của hàm số \(y = \cot x\) trên khoảng\(\;\left( {0;\pi } \right)\).
|
\(x\) |
\(\frac{\pi }{6}\) |
\(\frac{\pi }{4}\) |
\(\frac{\pi }{3}\) |
\(\frac{\pi }{2}\) |
\(\frac{{2\pi }}{3}\) |
\(\frac{{3\pi }}{4}\) |
\(\frac{{5\pi }}{6}\) |
|
\(y = \cot x\) |
? |
? |
? |
? |
? |
? |
? |
Bằng cách lấy nhiều điểm \(M\left( {x;\cot x} \right)\) với \(x \in \left( {0;\pi } \right)\) và nối lại ta được đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\).
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kỳ \(T = \pi \), ta được đồ thị của hàm số \(y = \cot x\) như hình dưới đây.
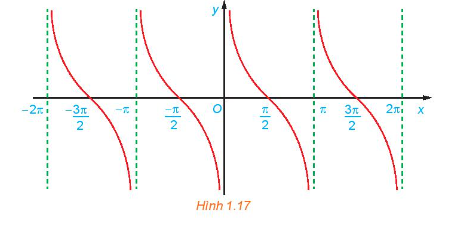
Từ đồ thị ở Hình 1.17, hãy tìm tập giá trị và các khoảng nghịch biến của hàm số \(y = \cot x\)
Hướng dẫn:
Sử dụng định nghĩa hàm số chẵn lẻ
Dựa vào đồ thị để xác định tập giá trị, các khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì -x cũng thuộc tập xác định D
Ta có: \(f\left( { – x} \right) = \cot \left( { – x} \right) = – \cot x = – f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \cot x\) là hàm số lẻ.
b)
|
\(x\) |
\(\frac{\pi }{6}\) |
\(\frac{\pi }{4}\) |
\(\frac{\pi }{3}\) |
\(\frac{\pi }{2}\) |
\(\frac{{2\pi }}{3}\) |
\(\frac{{3\pi }}{4}\) |
\(\frac{{5\pi }}{6}\) |
|
\(\cot x\) |
\(\sqrt 3 \) |
\(1\) |
\(\frac{{\sqrt 3 }}{3}\) |
\(0\) |
\( – \frac{{\sqrt 3 }}{3}\) |
\( – 1\) |
\( – \sqrt 3 \) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \cot x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\).