Đáp án Hoạt động 4 Bài 20. Hàm số mũ và hàm số lôgarit (trang 18, 19) – SGK Toán 11 Kết nối tri thức. Tham khảo: Vẽ đồ thị dựa vào các điểm đã lấy sau đó nhìn đồ thị để đưa ra tập giá trị.
Câu hỏi/Đề bài:
Cho hàm số lôgarit \(y = {\log _2}x.\)
a) Hoàn thành bảng giá trị sau:

b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_2}x} \right)\) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị của hàm số \(y = {\log _2}x\)
c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số \(y = {\log _2}x\)
Hướng dẫn:
Vẽ đồ thị dựa vào các điểm đã lấy sau đó nhìn đồ thị để đưa ra tập giá trị và tính chất biến thiên.
Lời giải:
a) Lập bảng giá trị của hàm số tại một điểm như sau:

b,
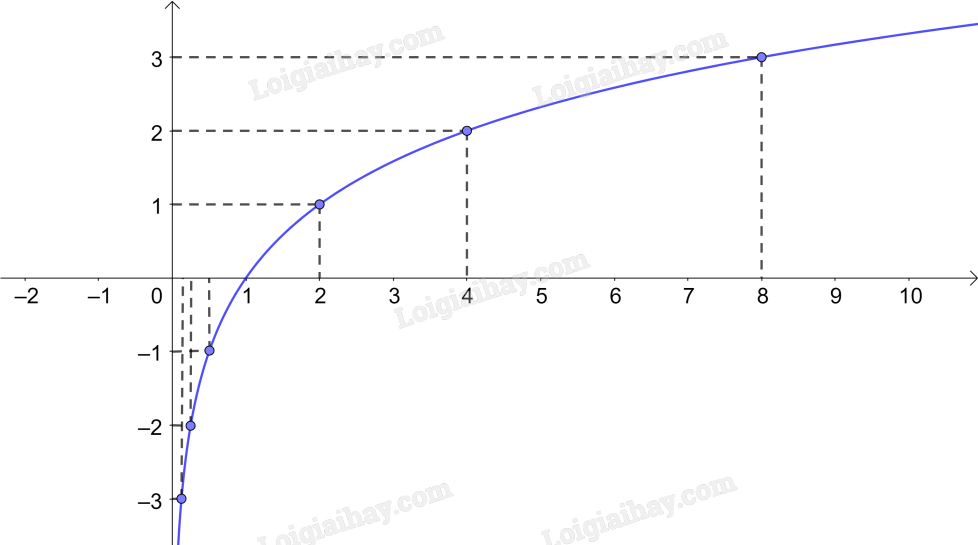
c) Tập giá trị: \(\mathbb{R}\)
Tính chất biến thiên: đồng biến