Giải Hoạt động 4 Bài 16. Giới hạn của hàm số (trang 115, 116, 117, 118) – SGK Toán 11 Kết nối tri thức. Tham khảo: Giả sử khoảng (a;b) chứa \({x_0}\) và hàm số \(y = f\left( x \right)\) xác định trên \(\left( {a.
Câu hỏi/Đề bài:
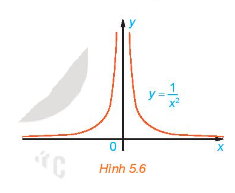
Xét hàm số \(f\left( x \right) = \frac{1}{{{x^2}}}\) có đồ thị như Hình 5.6. Cho \({x_n} = \frac{1}{n}\), chứng tỏ rằng \(f\left( {{x_n}} \right) \to + \infty \)
Hướng dẫn:
Giả sử khoảng (a;b) chứa \({x_0}\) và hàm số \(y = f\left( x \right)\) xác định trên \(\left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\). Ta nói hàm số \(f\left( x \right)\) có giới hạn \( + \infty \) khi \(x \to {x_0}\) nếu dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\},\;{x_n} \to {x_0}\), ta có \(f\left( {{x_n}} \right) \to + \infty ,\) kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = + \infty \)
Ta nói hàm số \(f\left( x \right)\) có giới hạn \( – \infty \) khi \(x \to \;{x_0}\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = – \infty \), nếu \(\mathop {\lim }\limits_{x \to {x_0}} \left[ { – f\left( x \right)} \right] = + \infty \)
Lời giải:
Ta có: \(\mathbb{R}\backslash \left\{ 0 \right\}\)
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} f\left( {{x_n}} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{{{\left( {\frac{1}{n}} \right)}^2}}} = \mathop {\lim }\limits_{x \to + \infty } {n^2} = + \infty \).
Vậy \(f\left( {{x_n}} \right) \to + \infty \).