Dựa vào đề bài để tìm ra công thức tổng quát. Hướng dẫn giải Bài 5.6 trang 109 SGK Toán 11 tập 1 – Kết nối tri thức – Bài 15. Giới hạn của dãy số. Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng (alpha ) (H.5.3)….
Đề bài/câu hỏi:
Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng \(\alpha \) (H.5.3). Từ A kẻ \(A{A_1} \bot BC\), từ \({A_1}\) kẻ \({A_1}{A_2} \bot AC\), sau đó lại kẻ \({A_2}{A_3} \bot BC\). Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn \(A{A_1}{A_2}{A_3} \ldots \) Tính độ dài đường gấp khúc này theo h và \(\alpha \)
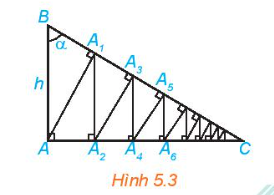
Hướng dẫn:
Dựa vào đề bài để tìm ra công thức tổng quát.
Lời giải:
Độ dài đường gấp khúc tạo thành cấp số nhân với số hạng tổng quát là:
\({u_n} = sin\;\alpha \; \times h \times {\left( {sin\;\alpha \;} \right)^{n – 1}}\).
Độ dài đường gập khúc: \(A{A_1} + {A_2}{A_3} + \ldots \).
Đây là tổng cấp số nhân lùi vô hạn với \({u_1} = sin\;\alpha \; \times h,\;q = sin\;\alpha \;\).
Nên \(A{A_1} + {A_2}{A_3} + \ldots = \frac{{sin\;\alpha \; \times h}}{{1 – sin\;\alpha \;}}\).