Nếu mặt phẳng (α)”>(α) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng phẳng (β)”>(β) thì (α)”>(α) và. Phân tích, đưa ra lời giải Bài 4.22 trang 94 SGK Toán 11 tập 1 – Kết nối tri thức – Bài 13. Hai mặt phẳng song song. Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là trung điểm của các cạnh AA’,…
Đề bài/câu hỏi:
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là trung điểm của các cạnh AA’, BB’, CC’. Chứng minh rằng mặt phẳng (MNP) song song với mặt phẳng (ABC).
Hướng dẫn:
Nếu mặt phẳng (α)”>(α) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng phẳng (β)”>(β) thì (α)”>(α) và (β)”>(β) song song với nhau.
Lời giải:
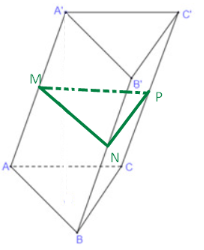
Ta có: ABB’A’ là hình bình hành, M, N là trung điểm của AA’, BB’ nên MN // AB (đường trung bình) suy ra MN // (ABC).
Tương tự, ta có NP // BC suy ra NP// (ABC).
Mặt phẳng (MNP) chứa hai đường thẳng cắt nhau MN, NP và MN, NP song song với mp(ABC) suy ra (MNP) //(ABC).