Hướng dẫn giải Hoạt động 3 Bài 2. Đường thẳng vuông góc với mặt phẳng (trang 57, 58, 59) – SGK Toán 11 Chân trời sáng tạo. Hướng dẫn: Sử dụng định lí 1: Nếu đường thẳng \(d\) vuông góc với hai đường thẳng cắt nhau \(a\.
Câu hỏi/Đề bài:
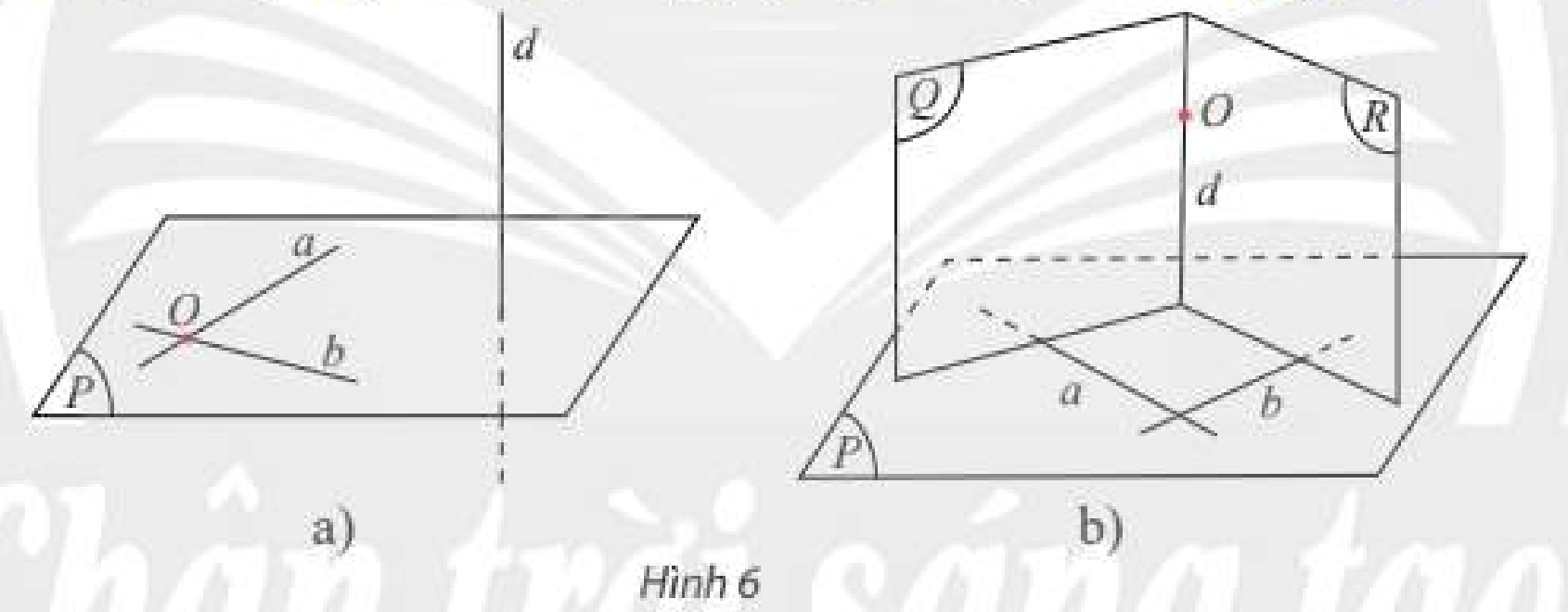
a) Trong không gian, cho điểm \(O\) và đường thẳng \(d\). Gọi \(a,b\) là hai đường thẳng phân biệt đi qua \(O\) và vuông góc với \(d\) (Hình 6a). Có nhận xét gì về vị trí tương đối giữa đường thẳng \(d\) và \(mp\left( {a,b} \right)\)?
b) Trong không gian, cho điểm \(O\) và mặt phẳng \(\left( P \right)\). Gọi \(\left( Q \right)\) và \(\left( R \right)\) là hai mặt phẳng đi qua \(O\) và lần lượt vuông góc với hai đường cắt nhau \(a,b\) nằm trong \(\left( P \right)\) (Hình 6b). Có nhận xét gì về vị trí giữa mặt phẳng \(\left( P \right)\) và giao tuyến \(d\) của \(\left( Q \right),\left( R \right)\)?
Hướng dẫn:
a) Sử dụng định lí 1: Nếu đường thẳng \(d\) vuông góc với hai đường thẳng cắt nhau \(a\) và \(b\) cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
b) Sử dụng tính chất: đường thẳng \(d\) vuông góc với mặt phẳng \(\left( \alpha \right)\) thì nó vuông góc với mọi đường thẳng \(a\) nằm trong \(\left( \alpha \right)\).
Lời giải:
a) Ta có:
\(\left. \begin{array}{l}d \bot a\\d \bot b\\a \cap b = \left\{ O \right\}\end{array} \right\} \Rightarrow d \bot mp\left( {a,b} \right)\).
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}a \bot \left( Q \right)\\d \subset \left( Q \right)\end{array} \right\} \Rightarrow a \bot d\\\left. \begin{array}{l}b \bot \left( R \right)\\d \subset \left( R \right)\end{array} \right\} \Rightarrow b \bot d\end{array}\)
Mà \(a,b\) cắt nhau nằm trong \(\left( P \right)\)
\( \Rightarrow d \bot \left( P \right)\)