Giải Hoạt động 2 Bài 3. Đường thẳng và mặt phẳng song song (trang 108, 109) – SGK Toán 11 Chân trời sáng tạo. Hướng dẫn: ‒ Để tìm giao tuyến của hai mặt phẳng.
Câu hỏi/Đề bài:
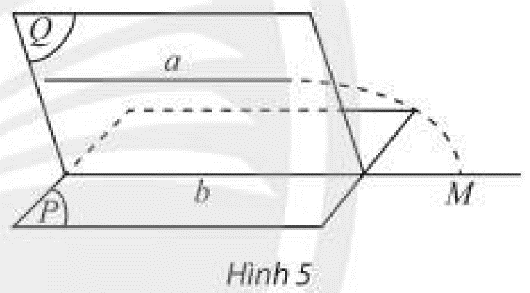
Cho đường thẳng \(a\) không nằm trong mặt phẳng \(\left( P \right)\) và \(a\) song song với một đường thẳng \(b\) nằm trong \(\left( P \right)\). Đặt \(\left( Q \right) = mp\left( {a,b} \right)\).
a) Tìm giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
b) Giả sử \(a\) có điểm chung \(M\) với \(\left( P \right)\) thì điểm \(M\) phải nằm trên đường thẳng nào? Điều này có trái với giả thiết \(a\parallel b\) hay không?
Hướng dẫn:
‒ Để tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung phân biệt hoặc một đường thẳng chung của hai mặt phẳng.
‒ Để tìm vị trí của điểm \(M\), ta sử dụng tính chất về giao tuyến của hai mặt phẳng.
Lời giải:
a) Ta có:
\(\left. \begin{array}{l}b \subset \left( P \right)\\b \subset \left( Q \right)\end{array} \right\} \Rightarrow b = \left( P \right) \cap \left( Q \right)\)
Vậy \(b\) là giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
b) Ta có:
\(\left. \begin{array}{l}M \in a\\a \subset \left( Q \right)\end{array} \right\} \Rightarrow M \in \left( Q \right)\)
Lại có: \(M \in \left( P \right)\)
Do đó điểm \(M\) nằm trên giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Vậy \(M \in b\).
Vậy \(M\) là một điểm chung của hai đường thẳng \(a\) và \(b\), trái với giả thiết \(a\parallel b\).