Hoạt động 1 Bài 4 (trang 25) Toán 11: Cho số thực t và M là điểm biểu diễn của góc lượng giác có số đo t rad trên đường tròn lượng giác

Câu hỏi/Đề bài:

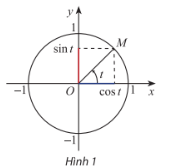
Cho số thực t và M là điểm biểu diễn của góc lượng giác có số đo t rad trên đường tròn lượng giác. Sử dụng định nghĩa của các giá trị lượng giác, hãy giải thích vì sao xác định duy nhất:

a) Giá trị sint và cost

b) Giá trị tant (nếu \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)) và \(\cot t\)(nếu \(t \ne k\pi ,k \in \mathbb{Z}\)).

Hướng dẫn:

Quan sát hình vẽ để trả lời.

Lời giải:

a) Ta thấy \(\sin t = {y_M}\) là tung độ của điểm M trên đường tròn lượng giác và c\(\cos t = {x_M}\) là hoành độ của điểm M trên đường tròn lượng giác.

Với mỗi điểm M xác định, ta chỉ có 1 tung độ và hoành độ duy nhất

Nên ta chỉ xác định duy nhất giá trị sint và cost.

b,

Nếu \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\), ta có: \(\tan t = \frac{{\sin t}}{{{\rm{cost}}}} = \frac{{{y_M}}}{{{x_M}}}\)( \({x_M} \ne 0\))

Nếu \(t \ne k\pi ,k \in \mathbb{Z}\), ta có: \(\cot t = \frac{{{\rm{cost}}}}{{{\rm{sint}}}} = \frac{{{x_M}}}{{{y_M}}}\)( \({y_M} \ne 0\))

Do \({x_M}\), \({y_M}\)xác định duy nhất nên \(\tan t\), \(\cot t\)xác định duy nhất.