Giải chi tiết Hoạt động 3 Bài 2. Giới hạn của hàm số (trang 66, 67, 68, 69) – SGK Toán 11 Cánh diều. Hướng dẫn: Quan sát đồ thị hình 6 để trả lời câu hỏi.
Câu hỏi/Đề bài:
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l} – 1,\,\,x 0\end{array} \right.\)
Hàm số \(f\left( x \right)\) có đồ thị ở Hình 6.
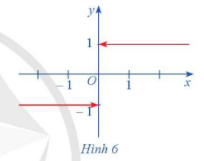
a) Xét dãy số \(\left( {{u_n}} \right)\) sao cho \({u_n} < 0\) và \(\lim {u_n} = 0.\) Xác định \(f\left( {{u_n}} \right)\) và tìm \(\lim f\left( {{u_n}} \right).\)
b) Xét dãy số \(\left( {{v_n}} \right)\) sao cho \({v_n} > 0\) và \(\lim {v_n} = 0.\) Xác định \(f\left( {{v_n}} \right)\) và tìm \(\lim f\left( {{v_n}} \right).\)
Hướng dẫn:
Quan sát đồ thị hình 6 để trả lời câu hỏi.
Lời giải:
a) Xét dãy số \(\left( {{u_n}} \right)\) sao cho \({u_n} < 0\) và \(\lim {u_n} = 0.\) Khi đó \(f\left( {{u_n}} \right) = – 1\) và \(\lim f\left( {{u_n}} \right) = – 1.\)
b) Xét dãy số \(\left( {{v_n}} \right)\) sao cho \({v_n} > 0\) và \(\lim {v_n} = 0.\) Khi đó \(f\left( {{v_n}} \right) = 1\) và \(\lim f\left( {{v_n}} \right) = 1.\)