Dùng định lí Ta lét và đường trung bình tam giác. Phân tích, đưa ra lời giải Bài 5 trang 104 SGK Toán 11 tập 1 – Cánh Diều – Bài 3. Đường thẳng và mặt phẳng song song. Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi M,…
Đề bài/câu hỏi:
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trọng tâm của hai tam giác ABF và ABC. Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACF).
Hướng dẫn:
Dùng định lí Ta lét và đường trung bình tam giác.
Lời giải:
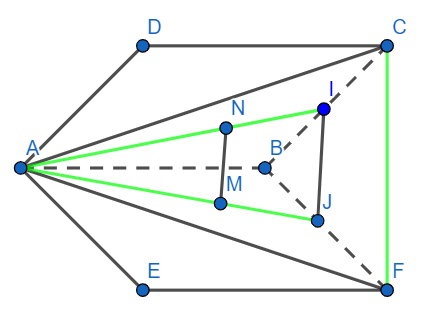
Gọi I,J lần lượt là trung điểm của BC, BF
Suy ra, IJ là đường trung bình của tam giác BCF.
Do đó, IJ // CF (1)
Tam giác AIJ có: \(\frac{{AM}}{{AI}} =\frac{{AN}}{{AJ}}= \frac{2}{3}\)
Suy ra, MN // IJ (theo Ta lét) (2)
Từ (1) và (2) suy ra MN // CF, mà CF nằm trong (ACF).
Suy ra MN // (ACF)