Dựa vào điều kiện đường thẳng vuông góc với mặt phẳng để chứng minh. Lời giải bài tập, câu hỏi Bài 3 trang 88 SGK Toán 11 tập 2 – Cánh Diều – Bài 2. Đường thẳng vuông góc với mặt phẳng. Cho tứ diện ABCD có (AB bot (BCD)), các tam giác BCD và ACD là những tam giác nhọn….
Đề bài/câu hỏi:
Cho tứ diện ABCD có \(AB \bot (BCD)\), các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD (Hình 31). Chứng minh rằng:
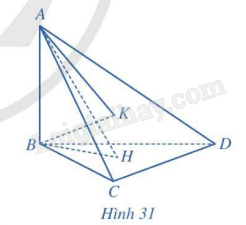
a) \(CD \bot (ABH)\)
b) \(CD \bot (ABK)\)
c) Ba đường thẳng AK, BH, CD cùng đi qua một điểm
Hướng dẫn:
Dựa vào điều kiện đường thẳng vuông góc với mặt phẳng để chứng minh
Lời giải:
a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có H là trực tâm của tam giác BCD \( \Rightarrow BH \bot CD\left( 2 \right)\)
Tử (1) và (2) \( \Rightarrow CD \bot \left( {ABH} \right)\)
b) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có K là trực tâm của tam giác BCD \( \Rightarrow AK \bot CD\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow CD \bot \left( {ABK} \right)\)
c) Ta có: \( CD \bot \left( {ABH} \right)\) và \(CD \bot \left( {ABK} \right)\). Mà theo tính chất 1, chỉ có duy nhất 1 mặt phẳng đi qua A và B vuông góc với CD. Nên \(\left( {ABH} \right) \equiv \left( {ABK} \right)\).
Ta có H là trực tâm của tam giác BCD nên BH giao với CD tại 1 điểm I, K là trực tâm của tam giác ACD nên AK giao với CD tại 1 điểm I’.
Mà (ABHK) cắt CD tại 1 điểm thuộc CD.
Nên I và I’ trùng nhau hay AK, BH, CD cùng đi qua một điểm.