Dựa vào quan hệ từ vuông góc đến song song trong không gian để chứng minh. Vận dụng kiến thức giải Bài 4 trang 88 SGK Toán 11 tập 2 – Cánh Diều – Bài 2. Đường thẳng vuông góc với mặt phẳng. Cho tứ diện ABCD có (AB bot (BCD),BC bot CD)….
Đề bài/câu hỏi:
Cho hình chóp S.ABCD có đáy là hình bình hành. Tam giác ABC nhọn có trực tâm H là hình chiếu của S trên (ABCD). Chứng minh rằng:
a) SA \(\bot\) AD;
b) SC \(\bot\) CD.
Hướng dẫn:
Dựa vào quan hệ từ vuông góc đến song song trong không gian để chứng minh
Lời giải:
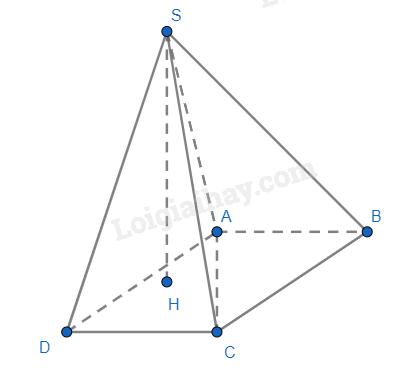
a) Vì SH \(\bot\) (ABCD) nên AH là hình chiếu của SA trên mặt phẳng (ABCD). Mà AH \(\bot\) BC, AD // BC => AH \(\bot\) AD. Theo định lí ba đường vuông góc ta có SA \(\bot\) AD.
b) Vì SH \(\bot\) (ABCD) nên HC là hình chiếu của SC trên mặt phẳng (ABCD). Mà AB \(\bot\) HC, AB // CD => HC \(\bot\) CD. Theo định lí 3 đường vuông góc ta có SC \(\bot\) CD.