Gọi \(A, B\) tương ứng là các biến cố: “Bạn \(An\. Giải và trình bày phương pháp giải Giải bài 8.14 trang 51 sách bài tập toán 11 – Kết nối tri thức với cuộc sống – Bài 30. Công thức nhân xác suất cho hai biến cố độc lập. Hai bạn An và Bình không quen biết nhau và đều học xa nhà…
Đề bài/câu hỏi:
Hai bạn An và Bình không quen biết nhau và đều học xa nhà. Xác suất để bạn An về thăm nhà vào ngày Chủ nhật là 0,2 và của bạn Bình là 0,25. Dùng sơ đồ hình cây để tính xác suất vào ngày Chủ nhật:
a) Cả hai bạn đều về thăm nhà.
b) Có ít nhất một bạn về thăm nhà.
c) Cả hai bạn đều không về thăm nhà.
d) Chỉ có bạn An về thăm nhà.
e) Có đúng một bạn về thăm nhà.
Hướng dẫn:
Gọi \(A,B\) tương ứng là các biến cố: “Bạn \(An\) về thăm nhà vào ngày Chủ nhật” và “Bạn Bình về thăm nhà vào ngày Chủ nhật”. \(A\) và \(B\) là hai biến cố độc lập.
Ta có sơ đồ hình cây:
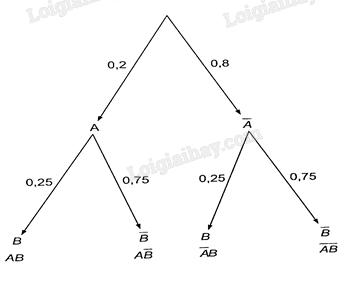
Từ đó suy ra xác suất cần tìm
Lời giải:
Gọi \(A,B\) tương ứng là các biến cố: “Bạn \(An\) về thăm nhà vào ngày Chủ nhật” và “Bạn Bình về thăm nhà vào ngày Chủ nhật”. \(A\) và \(B\) là hai biến cố độc lập.
Ta có sơ đồ hình cây:

a) \(P\left( {AB} \right) = 0,2 \cdot 0,25 = 0,05\).
b) \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {AB} \right) = 0,2 + 0,25 – 0,05 = 0,4\).
c) \(P\left( {\overline A \,\overline B } \right) = 0,8 \cdot 0,75 = 0,6\).
d) \(P\left( {A\overline B } \right) = 0,2 \cdot 0,75 = 0,15\).
e) \(P\left( {A\overline B \cup \overline A B} \right) = P\left( {A\overline B } \right) + P\left( {\overline A B} \right) = 0,2 \cdot 0,75 + 0,8 \cdot 0,25 = 0,35\).