Góc giữa 2 mặt phẳng cắt nhau là góc giữa 2 đường thẳng lần lượt nằm trên 2 mặt phẳng cùng vuông góc với giao. Trả lời Giải bài 7.45 trang 42 sách bài tập toán 11 – Kết nối tri thức với cuộc sống – Bài tập cuối Chương 7. Cho tứ diện đều \(ABCD\) có cạnh bằng\(a\), côsin của góc giữa hai mặt phẳng \(\left( {ACD} \right)\…
Đề bài/câu hỏi:
Cho tứ diện đều \(ABCD\) có cạnh bằng\(a\), côsin của góc giữa hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {BCD} \right)\)bằng
A. \(\frac{2}{3}\).
B. \(\frac{{\sqrt 3 }}{2}\).
C. \(\frac{{\sqrt 3 }}{3}\).
D. \(\frac{1}{3}\).
Hướng dẫn:
– Góc giữa 2 mặt phẳng cắt nhau là góc giữa 2 đường thẳng lần lượt nằm trên 2 mặt phẳng cùng vuông góc với giao tuyến của hai mặt phẳng.
– Áp dụng hệ quả định lý côsin trong tam giác
Lời giải:
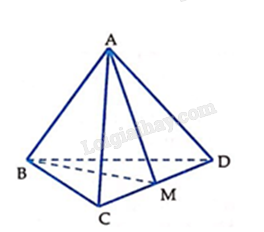
Ta có: \(\left( {ACD} \right) \cap \left( {BCD} \right) = CD\).
Gọi \(M\) là trung điểm \(CD\).
Khi đó dễ dàng chứng minh được \(BM \bot CD\) và \(AM \bot CD\).
\( \Rightarrow \left( {\left( {ACD} \right),\left( {BCD} \right)} \right) = \left( {AM,BM} \right)\).
Ta dễ tính được: \(AM = BM = \frac{{a\sqrt 3 }}{2}\).
Áp dụng hệ quả của định lý cô sin trong tam giác \(ABM\) ta có:
\(\cos \widehat {AMB} = \frac{{A{M^2} + B{M^2} – A{B^2}}}{{2.AM.BM}} = \frac{{\frac{{3{a^2}}}{4} + \frac{{3{a^2}}}{4} – {a^2}}}{{2.\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt 3 }}{2}}} = \frac{{\frac{{{a^2}}}{2}}}{{\frac{{3{a^2}}}{2}}} = \frac{1}{3}\).