Chóp có các cạnh bên bằng nhau có chân đường cao trùng với tâm đường tròn ngoại tiếp đáy. Gợi ý giải Giải bài 7.44 trang 42 sách bài tập toán 11 – Kết nối tri thức với cuộc sống – Bài tập cuối Chương 7. Cho tứ diện đều \(ABCD\)có cạnh bằng\(a\), côsin của góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\…
Đề bài/câu hỏi:
Cho tứ diện đều \(ABCD\)có cạnh bằng\(a\), côsin của góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\)bằng
A. \(\frac{1}{3}\).
B. \(\frac{{\sqrt 3 }}{3}\).
C. \(\frac{{\sqrt 3 }}{2}\).
D. \(\frac{1}{2}\).
Hướng dẫn:
– Chóp có các cạnh bên bằng nhau có chân đường cao trùng với tâm đường tròn ngoại tiếp đáy.
– Góc giữa đường và mặt là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng.
– Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.
Lời giải:
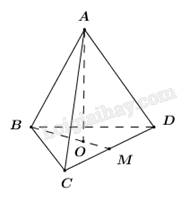
Gọi \(M\)là trung điểmcủa \(CD,O\) là tâm đường tròn ngoại tiếp tam giác đều \(BCD\)⇒\(AO \bot (BCD)\)
Khi đó \(OB\)là hình chiếu vuông góc của \(AB\) lên \((BCD)\)
\( \Rightarrow (AB;(BCD)) = (AB;OB) = \widehat {ABO}\)
Tam giác \(BCD\) đều cạnh a nên \(BM = \frac{{a\sqrt 3 }}{2} \Rightarrow BO = \frac{{2BM}}{3} = \frac{{a\sqrt 3 }}{3}\).
Ta có \(AO \bot (BCD)\) nên\(AO \bot OB\), suy ra \(\Delta ABO\)vuông tại \(O\).
⇒\(cos\widehat {ABO} = \frac{{OB}}{{AB}} = \frac{{\sqrt 3 }}{3}\)
Vậy \(\cos (AB;(BCD)) = \frac{{\sqrt 3 }}{3}\)