Bài 4.41 trang 71 SBT toán 11 – Kết nối tri thức: Cho hình lăng trụ tam giác ABC. A’B’C’. Gọi M là điểm thuộc cạnh BC sao cho MB = 2MC.

Đề bài/câu hỏi:

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M là điểm thuộc cạnh BC sao cho \(MB = 2MC.\)

a) Xác định hình chiếu M’ của M qua phép chiếu song song lên mặt phẳng (A’B’C’) theo phương AA’.

b) Chứng minh rằng \(M’B’ = 2M’C’\)

Hướng dẫn:

– Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(\Delta \) cắt \(\left( \alpha \right)\). Với mỗi điểm M trong không gian ta xác định điểm M’ như sau:

+ Nếu M thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và \(\Delta \).

+ Nếu M không thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và đường thẳng qua M song song với \(\Delta \).

Điểm M’ được gọi là hình chiếu của M trên mặt phẳng \(\left( \alpha \right)\) theo phương chiếu \(\Delta \).

– Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó; phép chiếu song song giữa nguyên tỉ số độ dài của hai đoạn thẳng cùng nằm trên một đường thẳng hoặc nằm trên hai đường thẳng song song.

Lời giải:

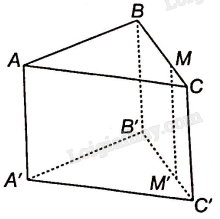
a) Trong mặt phẳng (BCC’B’) vẽ MM’//BB’ (M’ thuộc B’C’) thì M’ là hình chiếu của M qua phép chiếu đã cho.

b) Vì AA’//BB’//CC’ nên B’, C’ lần lượt là hình chiếu của B, C lên mặt phẳng (A’B’C’) theo phương chiếu AA’. Theo tính chất của phép chiếu song song suy ra \(\frac{{M’B’}}{{M’C’}} = \frac{{MB}}{{MC}} = 2\), suy ra \(M’B’ = 2M’C’\)