Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\. Giải và trình bày phương pháp giải Giải bài 4.36 trang 68 sách bài tập toán 11 – Kết nối tri thức với cuộc sống – Bài 13. Hai mặt phẳng song song. Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:…
Đề bài/câu hỏi:
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:
a) AB’//C’D’;
b) Hai mặt phẳng (AB’D’) và (C’B’D) song song với nhau.
Hướng dẫn:
Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.
Lời giải:
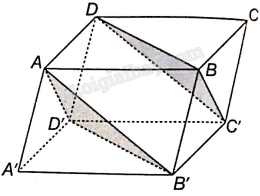
a) Tứ giác ABCD và BCC’B’ là hình bình hành nên AD//BC, \(AD = BC\) và BC//B’C’ và \(BC = B’C’\), do đó ADC’B’ là hình bình hành nên AB’//C’D.
b) Vì AB’//C’D nên AB’//mp(C’BD)
Chứng minh tương tự ta có: AD’//BC’ nên AD’//mp(C’BD). Mặt phẳng (AB’D’) có hai đường thẳng cắt nhau AB’ và AD’ cùng song song với mp(C’BD) nên hai mặt phẳng (AB’D’) và (C’B’D) song song với nhau.