Cho hai mặt phẳng song song, nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song. Lời giải bài tập, câu hỏi Giải bài 4.34 trang 68 sách bài tập toán 11 – Kết nối tri thức với cuộc sống – Bài 13. Hai mặt phẳng song song. Cho hình hộp ABCD.A’B’C’D’. Một mặt phẳng (P) cắt các cạnh AD, BC, B’C’, A’D’ lần lượt tại E, F,…
Đề bài/câu hỏi:
Cho hình hộp ABCD.A’B’C’D’. Một mặt phẳng (P) cắt các cạnh AD, BC, B’C’, A’D’ lần lượt tại E, F, G, H. Chứng minh rằng tứ giác EFGH là hình bình hành.
Hướng dẫn:
Cho hai mặt phẳng song song, nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Lời giải:
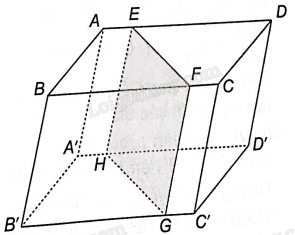
Vì hai mặt phẳng (ABCD) và (A’B’C’D’) của hình hộp song song với nhau nên giao tuyến của mặt phẳng (EFGH) và hai mặt phẳng đó song song với nhau, tức là EF//GH
Vì hai mặt phẳng (AA’D’D) và (B’B’C’B) của hình hộp song song với nhau nên giao tuyến của mặt phẳng (EFGH) và hai mặt phẳng đó song song với nhau, tức là EH//GF
Tứ giác EFGH có: EF//GH, EH//GF nên tứ giác EFGH là hình bình hành.