Chứng minh \(BD \bot \left( {SAC} \right)\) tại \(O\). Kẻ \(OH \bot SC, H \in SC\). Chứng minh \(OH\. Hướng dẫn giải Giải bài 21 trang 69 sách bài tập toán 11 – Kết nối tri thức với cuộc sống – Bài tập ôn tập cuối năm. Cho hình chóp đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\), cạnh bên \(SA\…
Đề bài/câu hỏi:
Cho hình chóp đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\), cạnh bên \(SA\) bằng \(a\sqrt 2 \). Khoảng cách giữa hai đường thẳng \(BD\) và \(SC\) là
A. \(\frac{{a\sqrt 6 }}{4}\).
B. \(\frac{{a\sqrt 6 }}{3}\).
C. \(\frac{{a\sqrt 6 }}{2}\).
D. \(\frac{{a\sqrt 3 }}{2}\).
Hướng dẫn:
Chứng minh \(BD \bot \left( {SAC} \right)\) tại \(O\). Kẻ \(OH \bot SC,H \in SC\).
Chứng minh \(OH\) là đoạn vuông góc chung của \(BD\) và \(SC\)
Tính \(OH\)
Lời giải:
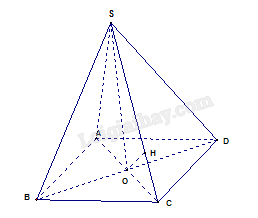
Ta có \(\left\{ \begin{array}{l}SO \bot \left( {ABCD} \right)\\BD \bot AC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}SO \bot BD\\BD \bot AC\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\)
Kẻ \(OH \bot SC,H \in SC\)
Ta có \(\left\{ \begin{array}{l}BD \bot \left( {SAC} \right)\\OH \subset \left( {SAC} \right)\end{array} \right. \Rightarrow OH \bot BD\)
Khoảng cách giữa hai đường thẳng \(BD\) và \(SC\) là \(OH\)
Có \(SO \bot AC \Rightarrow SO = \sqrt {S{A^2} – A{O^2}} = \sqrt {2{a^2} – {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 6 }}{2}\)
\(OH = \frac{{SO.OC}}{{\sqrt {S{O^2} + O{C^2}} }} = \frac{{\frac{{a\sqrt 6 }}{2}.\frac{{a\sqrt 2 }}{2}}}{{\sqrt {{{\left( {\frac{{a\sqrt 6 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} }} = \frac{{a\sqrt 6 }}{4}\)
Chọn A