Giải chi tiết Câu 5 Bài tập cuối chương 8 (trang 74, 75) – SBT Toán 11 Chân trời sáng tạo. Tham khảo: Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính.
Câu hỏi/Đề bài:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O. Cạnh bên \(SA = 2a\) và vuông góc với mặt phẳng đáy. Gọi \(\alpha \) là góc tạo bởi đường thẳng SC và mặt phẳng đáy. Khẳng định nào sau đây đúng?
A. \(\alpha = {60^0}\)
B. \(\alpha = {75^0}\)
C. \(\tan \alpha = 1\)
D. \(\tan \alpha = \sqrt 2 \)
Hướng dẫn:
Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính:
+ Nếu đường thẳng a vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a với (P) bằng \({90^0}\).
+ Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a và hình chiếu a’ của a trên (P) gọi là góc giữa đường thẳng a và (P).
Lời giải:
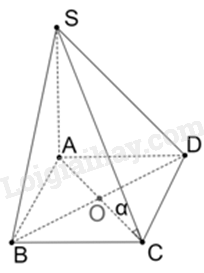
Vì \(SA \bot \left( {ABCD} \right)\) nên A là hình chiếu của S trên mặt phẳng (ABCD).
Do đó, \(\left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
Vì ABCD là hình vuông nên \(\widehat {ABC} = {90^0}\)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có: \(AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC\) nên tam giác SAC vuông tại A.
Suy ra: \(\tan \alpha = \frac{{SA}}{{AC}} = \frac{{2a}}{{a\sqrt 2 }} = \sqrt 2 \)
Chọn D