Giải chi tiết Câu 4 Bài tập cuối chương 4 (trang 132, 133) – SBT Toán 11 Chân trời sáng tạo. Hướng dẫn: Sử dụng kiến thức về giao điểm giữa đường thẳng và mặt phẳng để tìm giao tuyến.
Câu hỏi/Đề bài:
Cho hình chóp S. ABCD, đáy là hình bình hành có O là giao điểm của AC và BD. Gọi M, N lần lượt là các điểm nằm trên cạnh SC và SD. Đường thẳng SO cắt đường thẳng AM và BN lần lượt tại P và Q. Giao điểm của đường thẳng AM với mặt phẳng (SBD) là điểm nào sau đây?
A. Điểm P.
B. Điểm Q.
C. Điểm O.
D. Điểm M.
Hướng dẫn:
Sử dụng kiến thức về giao điểm giữa đường thẳng và mặt phẳng để tìm giao tuyến: Cách tìm giao điểm của đường thẳng d và mặt phẳng \(\left( \alpha \right)\):
– Trường hợp 1: Trong mặt phẳng \(\left( \alpha \right)\) có sẵn đường thẳng d’ cắt d tại I: Ta có ngay \(d \cap \left( \alpha \right) = I\)
– Trường hợp 2: Trong mặt phẳng \(\left( \alpha \right)\) không có sẵn đường thẳng d’ cắt d. Khi đó ta thực hiện như sau:
+ Chọn mặt phẳng phụ \(\left( \beta \right)\) chứa d và \(\left( \beta \right)\) cắt \(\left( \alpha \right)\) theo giao tuyến d’.
+ Gọi \(I = d’ \cap d\). Khi đó, \(d \cap \left( \alpha \right) = I\).
Lời giải:
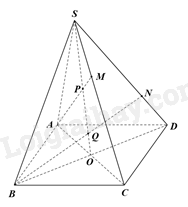
Vì P là giao điểm của AM và SO, mà \(SO \subset \left( {SBD} \right)\) nên P là giao điểm của AM và mặt phẳng (SBD).
Chọn A