Sử dụng kiến thức về giao tuyến giữa hai mặt phẳng để tìm giao tuyến. Hướng dẫn trả lời Giải bài 4 trang 112 sách bài tập toán 11 – Chân trời sáng tạo tập 1 – Bài 1. Điểm – đường thẳng và mặt phẳng trong không gian. Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy các điểm E, F,…
Đề bài/câu hỏi:
Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy các điểm E, F, G sao cho \(EB > AE,AF > FC,BG > GD\). Tìm giao tuyến của các cặp mặt phẳng (EFG) và (ACD), (EFG) và (BCD), (EFG) và (ABD).
Hướng dẫn:
Sử dụng kiến thức về giao tuyến giữa hai mặt phẳng để tìm giao tuyến: Đường thẳng d chung giữa hai mặt phẳng (P) và (Q) được gọi là giao tuyến của (P) và (Q), kí hiệu \(d = \left( P \right) \cap \left( Q \right)\).
Lời giải:
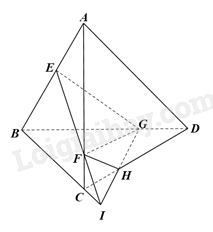
Ta có, EF là giao tuyến của hai mặt phẳng (EFG) và (ABC).
Trong mặt phẳng (ABC), gọi I là giao điểm của EF và BC.
Trong mặt phẳng (BCD), gọi H là giao điểm của IG và CD.
Vì \(\left\{ \begin{array}{l}H \in CD \subset \left( {ACD} \right),H \in IG \subset \left( {EFG} \right)\\F \in AC \subset \left( {ACD} \right),F \in FE \subset \left( {EFG} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (EFG) và (ACD) là FH.
Vì \(\left\{ \begin{array}{l}H \in CD \subset \left( {BCD} \right),H \in IG \subset \left( {EFG} \right)\\G \in BD \subset \left( {BCD} \right),G \in FG \subset \left( {EFG} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (EFG) và (BCD) là GH.
Vì \(\left\{ \begin{array}{l}E \in AB \subset \left( {ABD} \right),E \in FE \subset \left( {EFG} \right)\\G \in BD \subset \left( {ABD} \right),G \in FG \subset \left( {EFG} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (EFG) và (ABD) là GE.