Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để chứng minh. Giải và trình bày phương pháp giải Giải bài 2 trang 117 sách bài tập toán 11 – Chân trời sáng tạo tập 1 – Bài 2. Hai đường thẳng song song. Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB,…
Đề bài/câu hỏi:
Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\); I, J lần lượt là trung điểm của BD, CD.
a) Chứng minh rằng MN//BC.
b) Tứ giác MNJI là hình gì. Tìm điều kiện để tứ giác MNJI là hình bình hành.
Hướng dẫn:
Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để chứng minh: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
Lời giải:
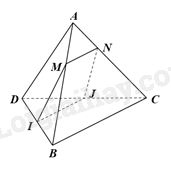
a) Tam giác ABC có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) nên MN//BC (định lí Thalès đảo)
b) Vì I, J lần lượt là trung điểm của BD, CD nên IJ là đường trung bình của tam giác BCD. Do đó, IJ//BC
Mà MN//BC nên IJ//MN, do đó, MNJI là hình thang.
Hình thang MNJI là hình bình hành khi và chỉ khi MI//NJ//AD.
Mà I là trung điểm của BD. Do đó, MI là đường trung bình của tam giác ADB.
Suy ra M là trung điểm của AB.