Sử dụng kiến thức về biểu diễn góc lượng giác trên đường tròn lượng giác. Giải và trình bày phương pháp giải Giải bài 11 trang 10 sách bài tập toán 11 – Chân trời sáng tạo tập 1 – Bài 1. Góc lượng giác. Cho ba điểm M, N, P lần lượt là các điểm biểu diễn trên đường tròn lượng giác của các…
Đề bài/câu hỏi:
Cho ba điểm M, N, P lần lượt là các điểm biểu diễn trên đường tròn lượng giác của các góc lượng giác có số đo \(k2\pi ,\frac{\pi }{2} + k2\pi ,\pi + k2\pi \left( {k \in \mathbb{Z}} \right)\). Tam giác MNP là tam giác gì?
Hướng dẫn:
Sử dụng kiến thức về biểu diễn góc lượng giác trên đường tròn lượng giác.
Lời giải:
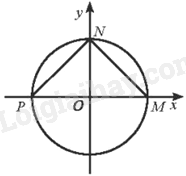
Vì điểm M biểu diễn trên đường lượng giác các góc lượng giác có số đo \(k2\pi \left( {k \in \mathbb{Z}} \right)\) nên \(M\left( {1;0} \right)\).
Vì điểm N biểu diễn trên đường lượng giác các góc lượng giác có số đo \(\frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\) nên \(N\left( {0;1} \right)\).
Vì điểm P biểu diễn trên đường lượng giác các góc lượng giác có số đo \(\pi + k2\pi \left( {k \in \mathbb{Z}} \right)\) nên \(P\left( { – 1;0} \right)\).
Do đó, \(PM = 2,NP = MN = \sqrt 2 \)
Vì \(M{N^2} + N{P^2} = P{M^2}\) nên tam giác MNP vuông N.
Lại có: \(NP = MN = \sqrt 2 \) nên tam giác MNP vuông cân tại N.