Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Nếu mặt phẳng (P) chứa hai đường thẳng a. Giải và trình bày phương pháp giải Giải bài 1 trang 127 sách bài tập toán 11 – Chân trời sáng tạo tập 1 – Bài 4. Hai mặt phẳng song song. Cho hình chóp S. ABCD có đáy là hình thang ABCD, AD//BC, \(AD = 2BC\). Gọi E, F,…
Đề bài/câu hỏi:
Cho hình chóp S. ABCD có đáy là hình thang ABCD, AD//BC, \(AD = 2BC\). Gọi E, F, I lần lượt là trung điểm của các cạnh SA, AD, SD.
a) Chứng minh (BEF)//(SCD) và CI//(BEF).
b) Tìm giao tuyến của hai mặt phẳng (SBC) và (SAD).
c) Tìm giao điểm K của FI với giao tuyến vừa tìm được ở câu b, từ đó chứng minh (SBF)//(KCD).
Hướng dẫn:
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng (Q) thì (P) song song với (Q).
Lời giải:
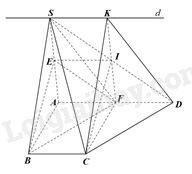
a) Vì E, F lần lượt là trung điểm của SA và AD nên EF là đường trung bình của tam giác SAD, suy ra EF//SD.
Mà \(SD \subset \left( {SCD} \right)\), EF không nằm trong mặt phẳng (SCD) nên EF//(SCD).
Vì F là trung điểm của AD nên \(AF = FD = \frac{1}{2}AD\), mà \(AD = 2BC\) nên \(BC = AF = FD\)
Lại có, BC//AD hay BC//DF.
Do đó, tứ giác BFDC là hình bình hành nên BF//CD.
Mà \(CD \subset \left( {SCD} \right)\), BF không nằm trong mặt phẳng (SCD) nên BF//(SCD).
Vì EF//(SCD), BF//(SCD), EF và BF cắt nhau tại F và nằm trong mặt phẳng (BEF)
Do đó, (BEF)//(SCD).
Vì E, I lần lượt là trung điểm của SA, SD nên EI là đường trung bình của tam giác SAD, do đó, EI//AD và \(EI = \frac{1}{2}AD\)
Mà AD//BC, \(BC = \frac{1}{2}AD\) nên EI//BC và \(EI = BC\). Do đó, tứ giác EICB là hình bình hành nên CI//BE
Mà \(BE \subset \left( {BEF} \right)\), CI không nằm trong mặt phẳng (BEF) nên CI//(BEF).
b) Ta có: BC//AD, \(BC \subset \left( {SBC} \right),AD \subset \left( {SAD} \right)\), mà \(S = \left( {SAD} \right) \cap \left( {SBC} \right)\).
Do đó, giao tuyến của hai mặt phẳng (SBC) và (SAD) là đường thẳng d đi qua S và song song song với BC, AD.
c) Vì \(d \subset \left( {SAD} \right),FI \subset \left( {SAD} \right)\) nên trong mặt phẳng (SAD), gọi K là giao điểm của FI và d.
Vì I, F lần lượt là trung điểm của SD, AD nên IF là đường trung bình của tam giác SAD. Do đó, IF//SA hay KF//SA
Mà SK//AF nên SKFA là hình bình hành. Do đó, \(SK = AF\)
Mà \(FD = AF\) nên \(SK = FD\)
Tứ giác SKDF có: \(SK = FD\), SK//DF nên SKDF là hình bình hành. Suy ra, SF//KD.
Vì SF//KD, \(KD \subset \left( {KCD} \right)\), SF không nằm trong mặt phẳng (KCD) nên SF//(KCD).
Vì BF//CD, \(CD \subset \left( {KCD} \right)\), BF không nằm trong mặt phẳng (KCD) nên BF//(KCD).
Lại có: SF và BF cắt nhau tại F và nằm trong mặt phẳng (SBF) nên (SBF)//(KCD).