Gọi \(H\) là trung điểm của cạnh \(BC\). Ta chứng minh \(H\) là hình chiếu của \(A\) trên mặt phẳng \(\left( {BCC’B’} \right)\). Gợi ý giải Giải bài 50 trang 110 sách bài tập toán 11 – Cánh diều – Bài 5. Khoảng cách. Cho hình hộp \(ABCD.A’B’C’D’\) có \(ABCD\) là hình thoi cạnh \(a\…
Đề bài/câu hỏi:
Cho hình hộp \(ABCD.A’B’C’D’\) có \(ABCD\) là hình thoi cạnh \(a\), \(AA’ \bot \left( {ABCD} \right)\), \(AA’ = 2a\), \(AC = a\). Tính khoảng cách:
a) Từ điểm \(A\) đến mặt phẳng \(\left( {BCC’B’} \right)\).
b) Giữa hai mặt phẳng \(\left( {ABB’A’} \right)\) và \(\left( {CDD’C’} \right)\).
c*) Giữa hai đường thẳng \(BD\) và \(A’C\).
Hướng dẫn:
a) Gọi \(H\) là trung điểm của cạnh \(BC\). Ta chứng minh \(H\) là hình chiếu của \(A\) trên mặt phẳng \(\left( {BCC’B’} \right)\), từ đó khoảng cách cần tìm là đoạn thẳng \(AH\).
b) Gọi \(I\) là trung điểm của cạnh \(DC\). Do \(\left( {ABB’A’} \right)\parallel \left( {DCC’D’} \right)\), nên khoảng cách giữa hai mặt phẳng này là khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {DCC’D’} \right)\). Ta chứng minh \(I\) là hình chiếu của \(A\) trên mặt phẳng \(\left( {DCC’D’} \right)\), từ đó khoảng cách cần tìm là đoạn thẳng \(AI\).
c) Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Gọi \(E\) là hình chiếu của \(O\) trên \(A’C\). Ta chứng minh \(OE\) là đường vuông góc chung của 2 đường thẳng \(BD\) và \(A’C\), từ đó khoảng cách cần tính là đoạn thẳng \(OE\).
Lời giải:
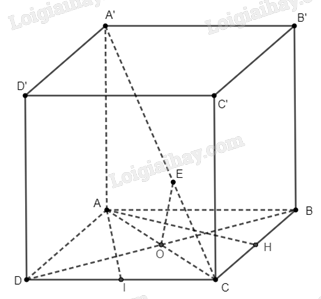
a) Gọi \(H\) là trung điểm của cạnh \(BC\). Tam giác \(ABC\) đều (\(AB = BC = AC = a\)) nên ta suy ra \(AH \bot BC\).
Do \(BB’ \bot \left( {ABCD} \right)\), ta suy ra \(BB’ \bot AH\).
Như vậy, do \(AH \bot BC\), \(BB’ \bot AH\) nên \(AH \bot \left( {BCC’B’} \right)\), điều này có nghĩa \(H\) là hình chiếu của \(A\) trên mặt phẳng \(\left( {BCC’B’} \right)\). Vậy khoảng cách từ \(A\) đến \(\left( {BCC’B’} \right)\) là đoạn thẳng \(AH\).
Tam giác \(ABC\) đều cạnh \(a\), đường cao \(AH\) nên \(AH = \frac{{a\sqrt 3 }}{2}\).
Vậy khoảng cách từ \(A\) đến \(\left( {BCC’B’} \right)\) là \(\frac{{a\sqrt 3 }}{2}\).
b) Do \(ABCD.A’B’C’D’\) là hình hộp, nên \(\left( {ABB’A’} \right)\parallel \left( {DCC’D’} \right)\). Suy ra khoảng cách giữa hai mặt phẳng này cũng bằng khoảng cách từ \(A\) đến mặt phẳng \(\left( {DCC’D’} \right)\).
Gọi \(I\) là trung điểm của cạnh \(DC\). Tam giác \(ADC\) có \(AB = DC = AC = a\) nên nó là tam giác đều. Suy ra \(AI \bot DC\) và \(AI = \frac{{a\sqrt 3 }}{2}\).
Do \(DD’ \bot \left( {ABCD} \right)\), ta suy ra \(DD’ \bot AI\). Như vậy, do \(AI \bot DC\), \(DD’ \bot AI\) nên \(AI \bot \left( {DCC’D’} \right)\). Điều này có nghĩa \(I\) là hình chiếu của \(A\) trên mặt phẳng \(\left( {DCC’D’} \right)\). Vậy khoảng cách giữa hai mặt phẳng \(\left( {ABB’A’} \right)\) và \(\left( {DCC’D’} \right)\), bằng khoảng cách từ \(A\) trên mặt phẳng \(\left( {DCC’D’} \right)\), là đoạn thẳng \(AI\), và bằng \(\frac{{a\sqrt 3 }}{2}\).
c) Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Do \(ABCD\) là hình thoi nên \(AC \bot BD\) và \(AO = \frac{{AC}}{2} = \frac{a}{2}\)
Do \(AA’ \bot \left( {ABCD} \right)\), nên \(AA’ \bot BD\). Như vậy, do \(AC \bot BD\), \(AA’ \bot BD\) nên \(\left( {AA’C} \right) \bot BD\).
Gọi \(E\) là hình chiếu của \(O\) trên \(A’C\). Vì \(OE \subset \left( {AA’C} \right)\), \(\left( {AA’C} \right) \bot BD\) nên \(OE \bot BD\). Như vậy \(OE\) là đường vuông góc chung của 2 đường thẳng \(BD\) và \(A’C\), điều này có nghĩa khoảng cách giữa \(BD\) và \(A’C\) là đoạn thẳng \(OE\).
Tam giác \(CEO\) và \(CAA’\) có chung góc \(C\) và có góc vuông \(\widehat {CEO} = \widehat {CAA’}\) nên chúng đồng dạng với nhau. Suy ra \(\frac{{OE}}{{AA’}} = \frac{{CO}}{{CA’}} \Rightarrow OE = \frac{{AA’.CO}}{{CA’}}\)
Tam giác \(AA’C\) vuông tại \(A\), nên \(A’C = \sqrt {A'{A^2} + A{C^2}} = \sqrt {{{\left( {2a} \right)}^2} + {a^2}} = a\sqrt 5 \).
Do đó \(OE = \frac{{AA’.OC}}{{A’C}} = \frac{{2a.\frac{a}{2}}}{{a\sqrt 5 }} = \frac{{a\sqrt 5 }}{5}\).